Inhalt
Wir wissen, dass ein elektrischer Strom durch einen Leiter ein Magnetfeld erzeugt. Lassen wir den Strom in einer Spule kreisen, erzeugen wir ein relativ starkes Magnetfeld im Inneren der Spule. Oft kann dieses Magnetfeld mit Hilfe eines sog. Kerns verstärkt werden, einem Material, das das Magnetfeld der Spule verstärkt.
Desweiteren wissen wir, dass ein sich änderndes Magnetfeld in einer Spule eine Spannung induziert.
Jetzt bringen wir diese beiden Aspekte zusammen und erzeugen mit einer sinusförmigen Wechselspannung einen sinusförmigen Wechselstrom. Dieser erzeugt ein ebenfalls oszillierendes Magnetfeld und damit einen oszillierenden magnetischen Fluss.
Der schwingende magnetische Fluss, der durch die erste Spule erzeugt wird, geht dann durch die zweite Spule (durch den Kern wird das Magnetfeld schön weiter geleitet und wir verlieren fast nicht davon). Weil sich der schwingende magnetische Fluss andauernd ändert, induziert er eine Wechselspannung, die ebenfalls oszilliert.
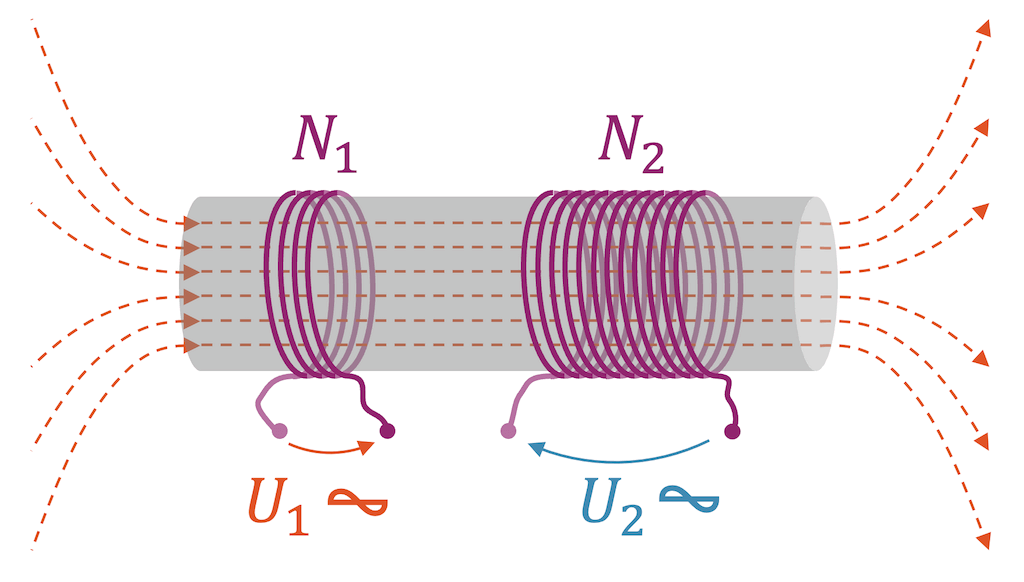
Zusammengefasst haben wir aus einer Wechselspannung \(U_1\) wieder eine Wechselspannung \(U_2\) gemacht. Das Spezielle daran ist, dass die Übertragung der Energie über ein ebenfalls schwingendes Magnetfeld geschah. Wir haben elektrische Arbeit zu elektrischer Arbeit gemacht, jedoch ohne elektrischen Kontakt dazwischen!
Mit der Gegeninduktion wird eine Wechselspannung \(U_1\) in der Primärspule über ein schwingendes Magnetfeld zu einer Wechselspannung \(U_2\) in der Sekundärspule umgewandelt. Dadurch wird elektrische Arbeit übertragen, ohne elektrischen (leitenden) Kontakt.
Über das Verhältnis der Windungen lässt sich das Verhältnis der Spannungen einstellen. Damit kann eine angelegte Wechselspannung \(U_1\) zu einer beliebigen Wechselspannung \(U_2\) hoch- oder heruntertransformiert werden. Die spannungswandelnden Transformatoren nutzen das Prinzip der Gegeninduktion.
Herleitung des Spannungsverhältnisses
Wenn wir eine Spannung an eine Spule anlegen, fliesst in ihr ein Strom, der dann ein Magnetfeld erzeugt. Gemäss Lenz’scher Regel induziert dieses Magnetfeld (wenn es sich aufbaut) als Reaktion eine Spannung, die ein entgegengesetztes Magnetfeld erzeugen würde. Diese induzierte Spannung gehorcht dem Induktionsgesetz:
\[ U_{ind} = – N_1 \cdot \frac{d\Phi_B}{dt} \]
Da die induzierte Spannung \(U_{ind}\) dem angelegten Magnetfeld entgegengesetzt ist, ist sie auch der Spannung \(U_1\) entgegen gesetzt, die dieses Magnetfeld aufbaut. Somit gilt:
\[ U_1 = -U_{ind} = N_1 \cdot \frac{d\Phi_B}{dt} \]
In der Sekundärspule ist es einfacher. Hier haben wir eine simple Induktionsspannung aufgrund des sich ändernden magnetischen Flusses \(\Phi_B\) im Kern. Wir schreiben hier einfach das Induktionsgesetz hin:
\[ U_2 = – N_2 \cdot \frac{d\Phi_B}{dt} \]
Wir lösen jetzt die beiden Ausdrücke für \(U_1\) und \(U_2\) nach \(\frac{d\Phi_B}{dt}\) auf, indem wir mit der Windungszahl \(N_1\) bzw. \(N_2\) dividieren. Dann setzen wir die beiden Ausdrücke gleich, denn es ist ja der gleiche, gemeinsame sich ändernde magnetische Fluss:
\[ \frac{d\Phi_B}{dt} = \frac{U_1}{N_1} = -\frac{U_2}{N_2} \]
Wir erhalten damit das Spannungsverhältnis zwischen den Spannungen \(U_1\) und \(U_2\). Üblicherweise wird die Gleichung noch so umgeformt, dass wir links die Spannungen haben und rechts das Verhältnis der Windungen. Wir multiplizieren dazu die Gleichung mit \(N_2\) und dividieren sie mit \(U_1\):
\[ \frac{U_2}{U_1} = – \frac{N_2}{N_1} \]
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.
Inhalt






Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.