Inhalt
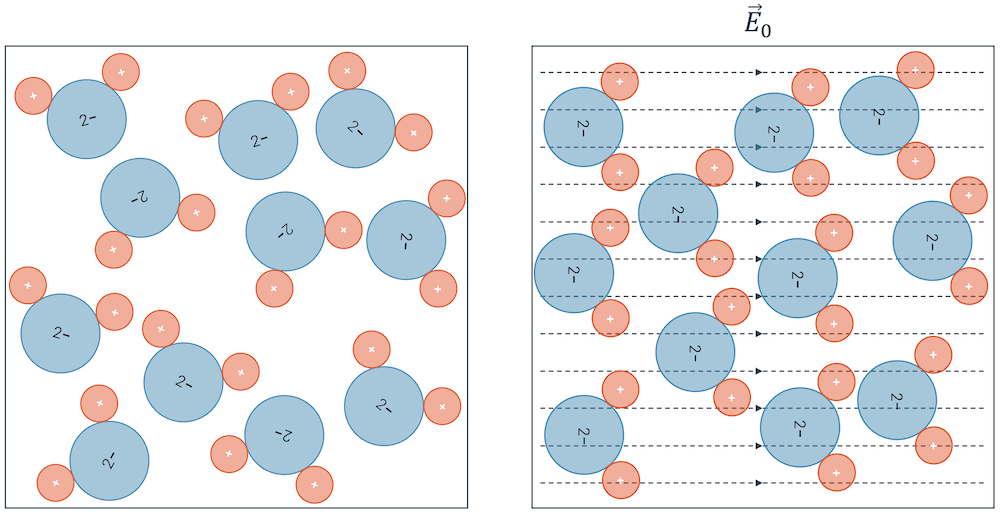
Isolierende Materialien haben keine freien Ladungsträger. Statt mit Influenz reagieren sie unter einem äusseren elektrischen Feld mit der Polarisation ihrer Ladungen. Die Ladungen verschieben sich und/oder orientieren sich im äusseren Feld. Dieses Verhalten wird dielektrisches Verhalten und das Material wird Dielektrikum genannt.
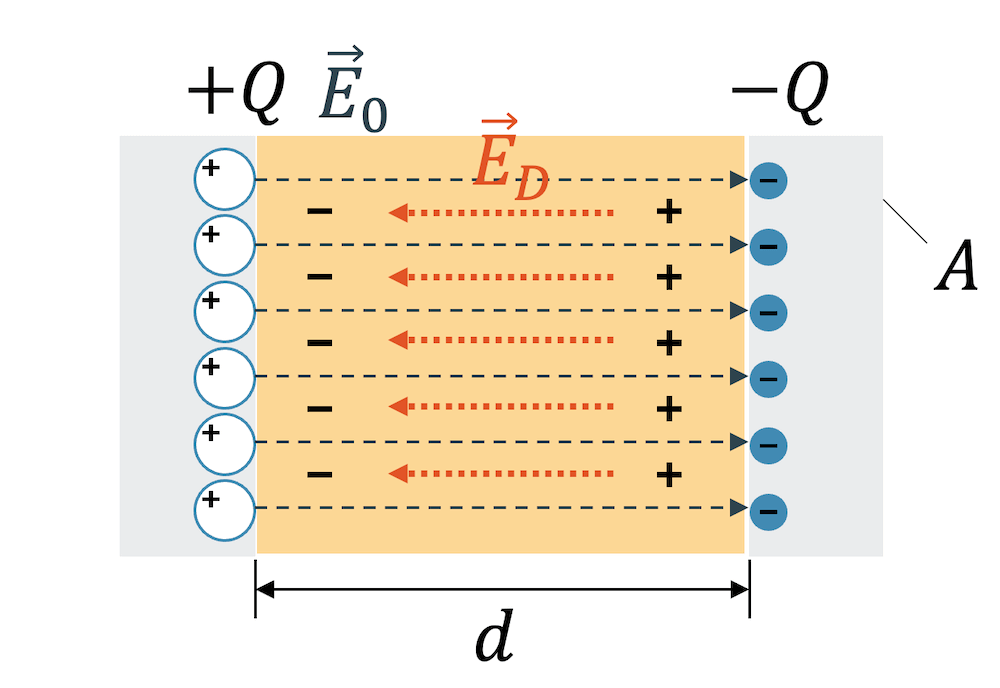
Im Dielektrikum entsteht ein inneres elektrisches Feld \(E_D\), das das äussere elektrische Feld \(E_0\) abschwächt. Die Abschwächung der Gesamtfeldstärke \(E_{res}\) wird mit dem Abschwächungsfaktor der relativen Dielektrizitätskonstante \(\varepsilon_r\) bemessen:
\[ E_{res} = \frac{E_0}{\varepsilon_r} \]
Für Kondensatoren hat die Abschwächung des elektrischen Felds zwischen den Platten die positive Wirkung, dass die Platten mehr Ladung bei gleicher Spannung aufnehmen können. Die relative Dielektrizitätskonstante ist für die Kapazität des Kondensators ein Vergrösserungsfaktor.
Verschiebungspolarisation
Aus der Chemie kennst du vielleicht den Begriff von unpolaren Molekülen. Ein einfaches kugelsymmetrisches Atom, wie z.B. das Atom eines Edelgases wäre ein perfektes Beispiel für unpolares Atom. Die Elektronenwolke verteilt sich um den Kern, so dass das Atom von jeder Seite ”gleich” aussieht – es gibt keine Richtung, die sich auszeichnet. Der Atomkern sitzt perfekt in der räumlichen Mitte der Wolke.
Wenn wir nun von aussen ein elektrisches Feld \(\vec{E}_0\) anlegen, dann wir der positive Kern eine Coulombkraft in Richtung des Felds erfahren. Die negative Elektronenwolke wird ebenfalls eine Coulombkraft spüren, jedoch in entgegengesetzter Richtung zu den Feldlinien.
Die Coulombkräfte des äusseren Felds ziehen an unserem Atom und möchten es auseinanderreissen. Die innere Coulombkraft zwischen Kern und Elektronenwolke wirkt aber weiterhin und hält Kern und Wolke zusammen. Es entsteht ein Kräftegleichgewicht und das Atom wird wie eine elastische Masse auseinandergezogen. Dieses Verschieben von Wolke und Kern nennen wir deshalb Verschiebungspolarisation.
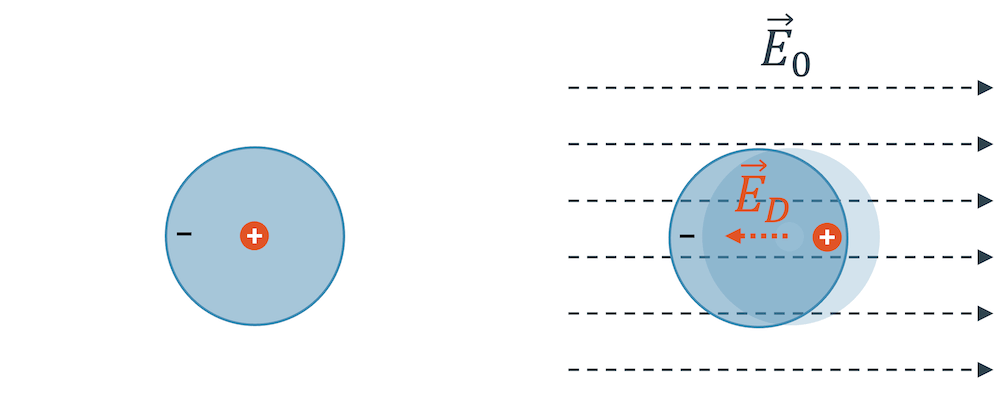
Die Zentren des positiven Kern und der negativen Elektronenwolke liegen nicht mehr übereinander. Zwischen ihnen entsteht ein inneres elektrisches Feld \(\vec{E}_D\), das dem äusseren Feld entgegengesetzt ist. Addieren wir die beiden Felder, erhalten wir das resultierende elektrische Feld, das gegenüber dem äusseren Feld abgeschwächt ist:
\[ \vec{E}_{res} = \vec{E}_{0} + \vec{E}_{D} \]
Orientierungspolarisation
Das Prinzip der Orientierungspolarisation ist ähnlich zur Verschiebungspolarisation. Der Unterschied liegt darin, dass wir ein bereits polares Molekül haben, das eine innere Ladungstrennung und damit bereits ein inneres elektrisches Feld \(E_D\) aufweist. Die Polarität des Moleküls ist nicht eine Folge des äusseren Felds, sondern liegt an der ungleichen Ladungsverteilung zwischen den Atomen innerhalb des Moleküls.
Legen wir wieder ein äusseres elektrisches Feld \(\vec{E}_0\) an, so wirken wieder Coulombkräfte auf die Atome im Molekül. Die positiven Atome werden in Richtung des äusseren Felds gezogen. Die negativen Atome zieht es in die andere Richtung. Da die Atome aber im Verband des Moleküls gefangen sind, wird sich das Molekül weder für die eine, noch für die andere Richtung entscheiden können, das es neutral ist. Es wird sich aber so abdrehen, dass die positiven Ladungen, in unserem Fall möglichst weit rechts und die negativen Ladungen möglichst weit links kommen. Wir nennen dieses Abdrehen in die Richtung des Felds deshalb die Orientierungspolarisation.
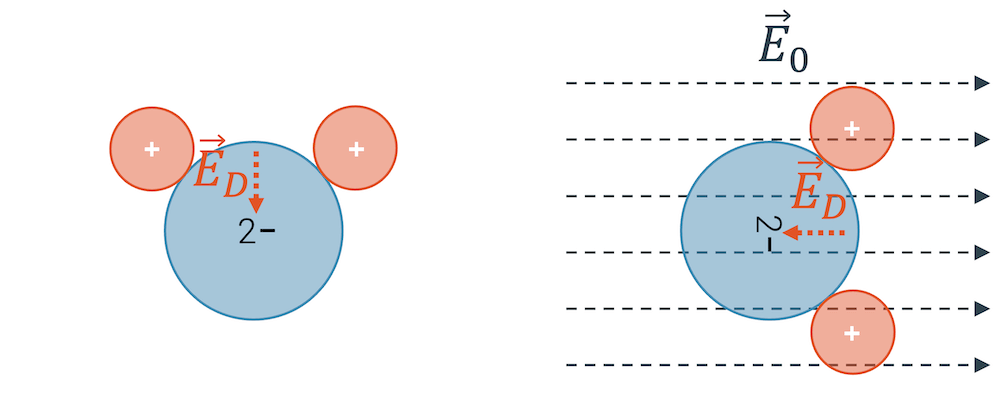
Das innere elektrische Feld \(\vec{E}_D\) wird mit dem Molekül umorientiert, so dass es wieder entgegengesetzt zum äusseren Feld zeigt. Für die Stärke des Gesamtfelds \(\vec{E}_{res}\) werden zwar die beiden Felder addiert, da die Richtungen aber entgegengesetzt sind, wird das Gesamtfeld gegenüber dem äusseren Feld abgeschwächt:
\[ \vec{E}_{res} = \vec{E}_{0} + \vec{E}_{D} \]
Beachte, dass die polaren Moleküle schon von Anfang an ein inneres elektrisches Feld haben. Sie sind aber alle zufällig ausgerichtet. Die Summe all dieser inneren elektrischen Felder ist deshalb null, weil sie sich gegenseitig aufheben. Mikroskopisch gesehen (Betrachtung von nur einem Molekül) haben wir durchaus ein inneres elektrisches Feld. Makroskopisch gesehen (Betrachtung einer bestimmten Menge an Material) haben wir kein elektrisches Feld.
Durch die Ausrichtung der Moleküle im äusseren elektrischen Feld, entfaltet das innere Feld erstmals eine Wirkung. Aus makroskopischer Sicht entsteht ein inneres elektrisches Feld, das vor der Ausrichtung nicht da war.
Makroskopische Polarisation
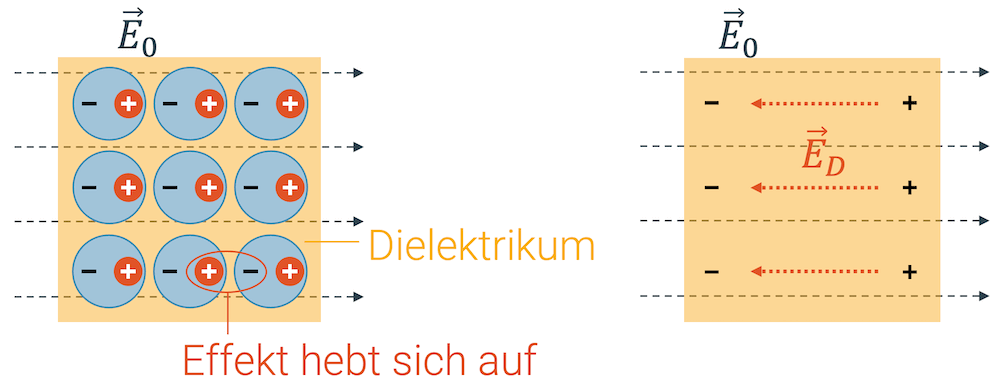
Wenn wir unsere Betrachtungen der Verschiebungs- und der Orientierungspolarisation nehmen und etwas ”herauszoomen”, können wir verallgemeinern, dass das äussere elektrische Feld \(\vec{E}_0\) in beiden Fällen durch ein inneres elektrisches Feld \(\vec{E}_D\) abgeschwächt wird. Die Addition der Feldvektoren ist für den Betrag des Gesamtfelds eigentlich eine Subtraktion, da das innere elektrische Feld dem äusseren Feld entgegenwirkt:
\[ \vec{E}_{res} = \vec{E}_{0} + \vec{E}_{D} \qquad \rightarrow \qquad E_{res} = E_0 – E_D \]
Wenn \(E_{res}\) kleiner als \(E_0\) ist, dann können wir auch schreiben, dass das Gesamtfeld \(E_{res}\) um einen Faktor \(\varepsilon_r\) verkleinert wird:
\[ E_{res} = \frac{E_0}{\varepsilon_r} \]
Wir nennen diesen Faktor relative Dielektrizitätskonstante \(\varepsilon_r\). Es ist eine Zahl ohne Einheit. Sie ist der Abschwächungsfaktor für das elektrische Feld im Dielektrikum. Die relative Dielektrizitätskonstante wurde für viele Materialien gemessen und kann in Tabellen nachgeschaut werden. Nachfolgend sind die relativen Dielektrizitätskonstanten \(\varepsilon_r\) für ein paar besondere Stoffe aufgeführt:
| Stoff | Relative Dielektrizitätskonstante \(\varepsilon_r\) |
| Vakuum | 1 |
| Luft | 1.0005 |
| Glas | 4 bis 10 |
| Porzellan | 6 |
| Wasser | 80.1 |
| Seignette-Salz | 9’000 |
| Bariumtitanat | 10’000 |
Vakuum ist der Referenzwert, wo überhaupt keine Polarisation stattfindet und wir deshalb keinerlei Abschwächung haben. Luft verhält sich praktisch wie Vakuum. Metalle sind hier nicht aufgeführt, denn sie erlauben durch ihre sehr hohe Leitfähigkeit keine Polarisation. Die freien Ladungsträger werden durch das äussere Feld bewegt und nicht nur verschoben. Es kann sich kein inneres Feld aufbauen.
Einsatz von Dielektrika in Kondensatoren
Aus der Tabelle der relativen Dielektrizitätskonstanten \(\varepsilon_r\) können wir sehen, dass extrem starke Abschwächung bei ganz speziellen Stoffen möglich sind. Bariumtitanat wird beispielsweise in sehr starken Kondensatoren, sog. ”Supercaps” eingesetzt.
Durch die Abschwächung des elektrischen Felds im Kondensator ist auch die Spannung entsprechend abgeschwächt. Wir können eine viel grössere Ladungsmenge an den Platten aufbauen und die Spannung nimmt kaum zu. im \(U,Q\)-Diagramm ist der Verlauf extrem flach, was einer grösseren Kapazität \(C\) des Kondensators entspricht.
Wir können, dank dem dielektrischen Material, viel mehr Ladung auf den Kondensator bringen, bevor wir die maximale Spannung erreicht haben. Der Abschwächungsfaktor \(\varepsilon_r\) für das elektrische Feld und die Spannung erweist sich als Verstärkungsfaktor für die Kapazität. Für den Plattenkondensator schreiben wir deshalb:
\[ C = \varepsilon_0 \frac{A}{d} \qquad \rightarrow \qquad C = \varepsilon_r \cdot \varepsilon_0 \frac{A}{d} \]
Für den Einsatz in Kondensatoren muss natürlich auch sichergestellt werden, dass kein Ladungsfluss stattfindet, d.h. dielektrische Flüssigkeiten mit Ladungsträgern (Ionen) fallen dafür weg.
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.
Inhalt






Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.