Streulinse (Zerstreuungslinse)

Streulinsen (oft auch Zerstreuungslinsen oder bikonkave Linsen genannt) sind in der Mitte dünner als aussen (konkav). Durch die Brechung werden die Lichtstrahlen in der Streulinse so umgelenkt, dass parallele Strahlen nach der Linse auseinander driften oder eben gestreut.

Streulinsen finden wir z.B. als Korrekturgläser für Kurzsichtige 👓. Sie finden sich aber auch in Objektiven und anderen optischen Instrumenten.

Ähnlich wie Konvexspiegel, erzeugen Streulinsen ein verkleinertes Bild, das aber mehr Übersicht vermittelt. Typischerweise sehen wir die Umgebung unter einem grösseren Winkel und gerade Linien werden so verzogen, dass sie gekrümmt sind.

Brennpunkt und Brennweite einer Streulinse

Die Funktionsweise der Streulinse können wir mit Hilfe von Prismen verstehen. Die beiden parallelen Strahlen werden nach aussen ausgelenkt und verlaufen danach auch nicht mehr parallel, sondern leicht auseinander. Deren gemeinsamer, aber nur scheinbarer Ursprungsort ist der Brennpunkt \(F\). Es handelt sich um einen virtuellen Brennpunkt. Die Strahlen sind nie wirklich im Brennpunkt. Es ist deshalb unmöglich, dass Sonnenlicht auf eine Streulinse jemals einen Brand verursachen könnte.

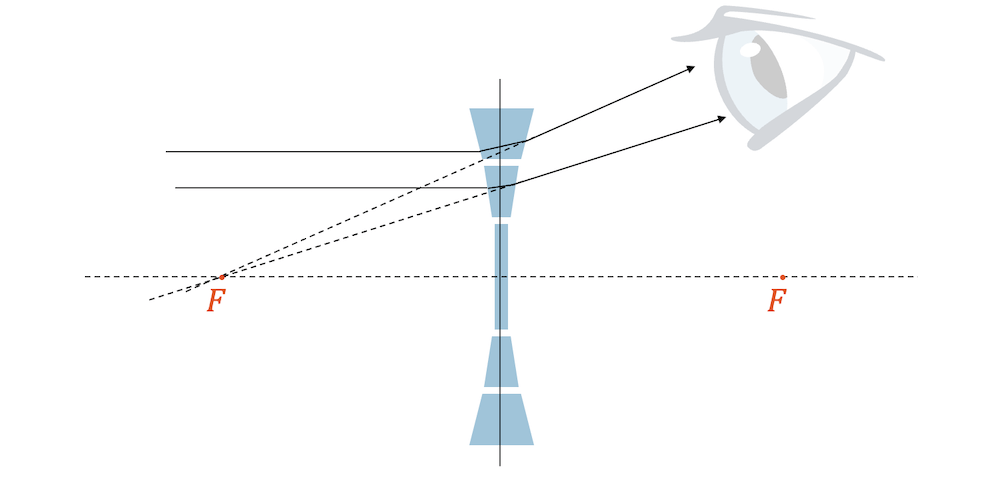
Dank dem Brechungsgesetz verstehen wir, dass die parallelen Strahlen nach der Linse auseinander laufen. Nur der Lichtstrahl auf der optischen Achse trifft genau senkrecht auf das Medium der Linse und behält deshalb seine Richtung.

Die Parallelstrahlen verlaufen nach der Streulinse in der Art, als kämen sie alle aus dem Brennpunkt \(F\). Es gilt deshalb auch hier die Regel:

Parallelstrahlen werden durch die Streulinse umgelenkt zu Brennpunktstrahlen

Brennpunktstrahlen werden durch die Streulinse umgelenkt zu Parallelstrahlen

Auch die Streulinsen haben immer zwei Brennpunkte, die auf der optischen Achse und im gleichen Abstand von der Linsenebene liegen (Brennweite \(f\)). Stark gekrümmte Linsen brechen die Strahlen stark und haben eine kurze Brennweite.

Entstehung eines virtuellen Bildes

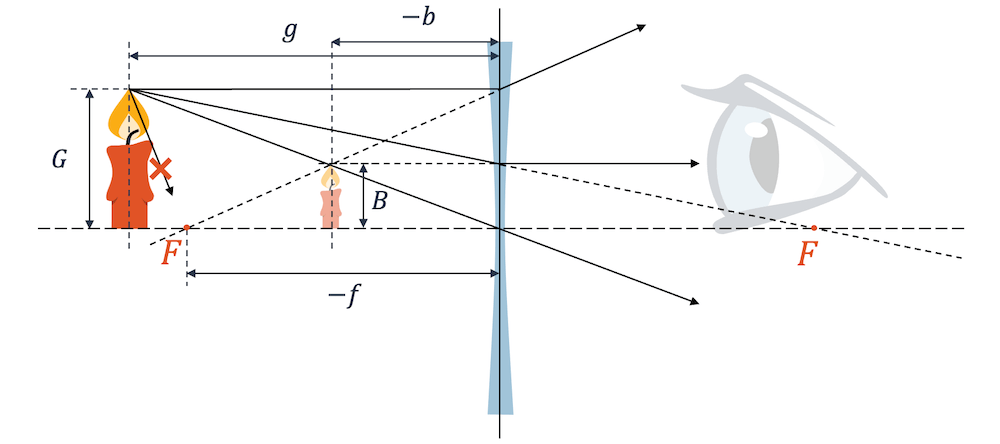
Wir betrachten wieder eine Kerze als unseren Gegenstand. Die Flammenspitze sendet Lichtstrahlen in alle Richtungen. Wir brauchen aber nur zwei spezielle Strahlen, um einen Bildpunkt zu kriegen.

Wir können sicher den Parallelstrahl nehmen und ihn zu einem Brennpunktstrahl machen.

Der Brennpunktstrahl würde auch gehen, allerdings muss hier beachtet werden, den richtigen Brennpunkt zu verbinden. Die Streulinse hat einen virtuellen Brennpunkt. Wir dürfen deshalb nicht den linken Brennpunkt wählen, sondern müssen den unerreichbaren Brennpunkt auf der anderen Seite der Linse nehmen. Nur die Verlängerung erreicht ihn; der physikalische Strahl wird an der Linse gebrochen.

Grundsätzlich gibt es auch bei der Streulinse den Scheitelpunktstrahl, den du vermutlich vom Konkavspiegel kennst. Er wird oft auch Mittelpunktstrahl genannt, doch diese Bezeichnung wäre problematisch, wenn wir sie beim Konkavspiegel anwenden wollten, weil es dort einen anderen Strahl gibt, der so heisst.

Beim Konkavspiegel haben wir für den Scheitelpunktstrahl mit dem Reflexionsgesetz argumentiert und gesagt, dass er mit gleichem Winkel reflektiert wird (Reflexionswinkel), wie er auf den Spiegel eingefallen ist (Einfallswinkel).

Bei der Linse haben wir keine Reflexion, aber der Scheitelpunktstrahl ist sehr praktisch, weil einfach zu zeichnen. Er wird ungebrochen durch die Linsenebene gezeichnet. Er verhält sich analog zum Spiegel, d.h. er verlässt die Linsenebene in gleichem Winkel, wie er auf sie aufgetroffen ist.

In Realität verläuft der Strahl parallel zum ursprünglichen Strahl, aber leicht versetzt. Die Dicke der Linse bestimmt, wie stark versetzt der Strahl nach der Linse ist. Da wir aber von sehr dünnen Linsen ausgehen, vernachlässigen wir diesen Effekt.

Beachte auch: Es ist in der Optik üblich, die Brechung nur mit einer einzige Brechung in der Linsenebene darzustellen. Oft wird der Linsenkörper gar nicht gezeichnet. Wir haben den Linsenkörper hier im Hintergrund angedeutet, damit wir nicht vergessen, um welche Art von Linse es sich handelt. 🧐

Der Beobachter sieht jetzt drei Strahlen und alle kommen scheinbar aus einem virtuellen Bildpunkt. Wir können deshalb das virtuelle Bild der Kerze aufzeichnen. Es ist, wie erwartet, verkleinert und aufrecht.

Bei der Streulinse gibt es immer virtuelle, aufrechte Bilder, die kleiner sind als der Gegenstand selber.

Im Vergleich zur Sammellinse gibt es keinen “Kipppunkt”, wo ein aufrechtes Bild zu einem umgekehrten Bild wechselt oder umgekehrt. Wir können den Gegenstand auch ganz nahe an die Linse heranbringen. Im Gegensatz zur Sammellinse sind wir mit dem Gegenstand nicht über den entscheidenden Brennpunkt gegangen, sondern nur etwas näher an den virtuellen Brennpunkt auf der anderen Seite der Linse.

Linsengleichung

Für Streulinsen gilt die Linsengleichung auch. Sie erlaubt z.B. die Berechnung der Bildweite \(b\) aus der Gegenstandsweite \(g\) und der Brennweite \(f\) der Linse. Die Brennweite wird aber mit einem negativen Betrag eingesetzt, da der Brennpunkt virtuell ist, d.h. auf der “falschen” Seite der Linse ist:

\[ \frac{1}{f} = \frac{1}{g} + \frac{1}{b} \quad \mathrm{mit} \quad f<0 \]

Da das Bild virtuell ist, wird auch die berechnete Bildweite \(b\) negativ sein. Gemeint ist damit, dass auch das Bild sich auf der “falschen Seite” der Linse befindet.

Beispiel

Ein \(g=12\,\mathrm{cm}\) grosser Gegenstand steht im Abstand \(g=10\,\mathrm{cm}\) vor einer Streulinse mit Brennweite \(f=-30\,\mathrm{cm}\). Wie weit erscheint das Bild des Gegenstands für den Betrachter, wenn er ihn durch die Linse anschaut? Wie gross ist das Bild?  

Lösung

Mit der Linsengleichung erhalten wir: \[ \frac{1}{b} = \frac{1}{f} \;-\; \frac{1}{g} \] \[ \frac{1}{b} \;=\; \frac{g-f}{fg} \] Nun bilden wir den Kehrwert von \(\frac{1}{b}\) und erhalten: \[ b = \frac{fg}{g-f} = \frac{(-0.3\,\mathrm{m}) \cdot 0.1\,\mathrm{m}}{0.1\,\mathrm{m} \;-\; (-0.3\,\mathrm{m})} \] \[ b = \frac{-0.03\,\mathrm{m^2}}{0.4\,\mathrm{m}} = -\frac{0.03}{0.4}\mathrm{m} \] \[ b = -0.075\,\mathrm{m} = \underline{-7.5\,\mathrm{cm}} \] Das Bild ist 7.5 cm vor der Linse. Die Bildweite ist (wie die Brennweite) negativ, weil das Bild ein virtuelles Bild vor der Linse ist. Für die Ermittlung der Grösse des Bilds \(B\) betrachten wir die beiden rechtwinkligen Dreiecke, die mit dem Scheitelpunktstrahl entstehen: Das erste Dreieck hat die Höhe \(G\) und die Grundseite \(g\). Die Höhe des zweiten Dreiecks ist \(B\) und die Grundseite ist \((-b)\), da \(b\) negativ ist. Beide Dreiecke sind ähnlich, so dass deren Seiten gemäss Strahlensatz zu einander proportional sind. Wir können deshalb schreiben: \[ \frac{G}{g} = \frac{B}{(-b)} \] Wir lösen nach der Unbekannten \(B\) auf indem wir mit \((-b)\) multiplizieren und setzen die Zahlenwerte ein: \[ B = \frac{(-b)}{g} \cdot G = \frac{0.075\,\mathrm{m}}{0.1\,\mathrm{m}} \cdot 0.12\,\mathrm{m} \] \[ B = 0.09\,\mathrm{m} = \underline{9\,\mathrm{cm}} \] Dieses Resultat ist typisch für eine Streulinse: Das Bild ist kleiner und näher zum Betrachter, als der Gegenstand.

Simulation

Mit der folgenden Simulation kannst du die Entstehung von reellen und virtuellen Bildern und die ganze Strahlenkonstruktion sehr einfach nachvollziehen. Es lohnt sich ein bisschen damit herum zu spielen, um ein Gefühl für die richtigen Strahlenläufe zu entwickeln.

Bewege die Spitze des Gegenstands Object mit der Maus. Der Brennpunkt wird verändert, indem du das Label Focus‘ verschiebst.

Simulation der Strahlenverläufe durch eine Sammel- bzw. Streulinse