Kraftwandler

Was sind Kraftwandler?

Kraftwandler machen genau das, was ihr Name sagt: Sie sind eine mechanische Einrichtung, die Kräfte umwandelt, d.h. sie machen aus einer kleinen Kraft eine grosse Kraft oder umgekehrt.

Mit Hilfe von Kraftwandlern kann z.B. der Mensch Kräfte erzeugen, die um ein Vielfaches grösser sind als, was der menschliche Körper je erreichen könnte. Dadurch können z.B. schwere Lasten angehoben werden (z.B. Wagenheber).

Die meisten Maschinen benutzen Kraftwandler um noch stärker zu sein als der eingebaute Motor. Mit Getrieben (Kraftwandler) werden Motoren manchmal auch schwächer, dafür schneller gemacht.

Kraftwandler wandeln Kräfte um:

• Kräfte verstärken (dafür kleinere Wege)
• Kräfte abschwächen (dafür grössere Wege, grössere Geschwindigkeit)

Im Alltag gibt es sehr viele Beispiele von Kraftwandlern, Meistens benutzen sie das Hebelgesetz in irgendeiner Form.

Mit dem Nussknacker können wir mit Hilfe des Hebelgesetzes eine grössere Kraft \(F_2\) erreichen und damit die harte Nussschale knacken. Für uns ist es wichtig, dass wir selber nur die kleine Kraft \(F_1\) aufbringen müssen. Der Nussknacker wandelt diese Kraft um, so dass wir die Nuss mit einer viel grösseren Kraft knacken.

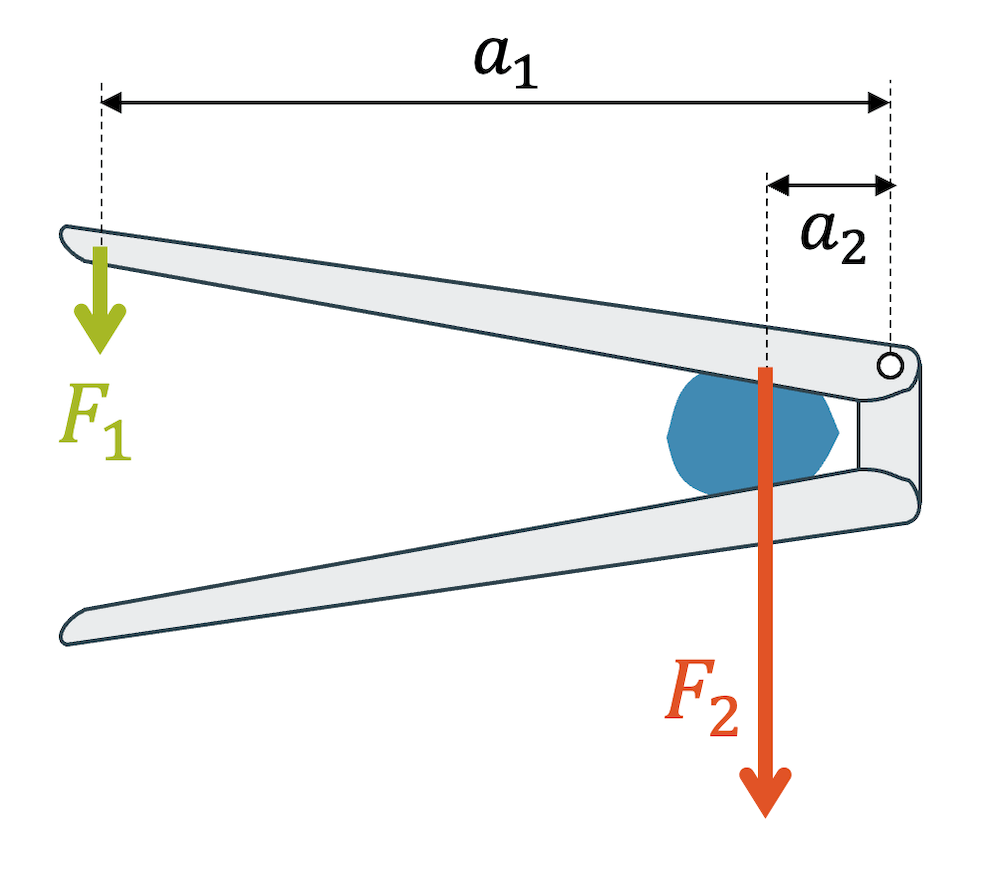
Im Hebelgesetz finden wir den Verstärkungsfaktor, der durch die unterschiedlichen Abstände \(a_1\) und \(a_2\) entsteht:

\[ F_2 = \frac{a_1}{a_2} \cdot F_1 \]

Beim Gangschaltung eines Fahrrads (Getriebe) ist die Kraft auf die Kette \(F_2\) rund doppelt so gross wie die Tretkraft \(F_1\), d.h. nur schon die Pedale ist bereits ein “Hebel” bzw. ein Kraftwandler.

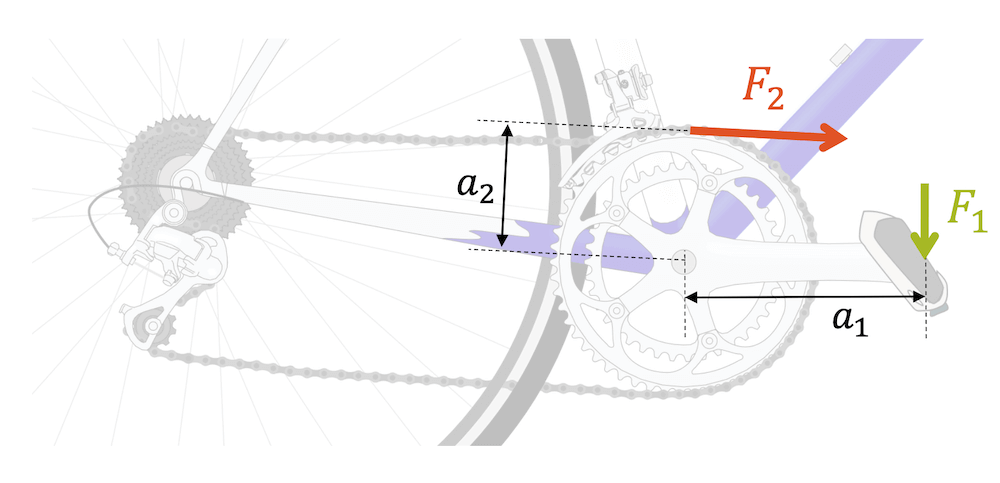
Die Gangschaltung beim Fahrrad ist ein einfaches Getriebe. Es erlaubt unterschiedliche Verstärkungsfaktoren zu wählen, je nachdem ob viel Weg (grosse Geschwindigkeit) oder viel Kraft gebraucht werden.

Goldene Regel der Mechanik

Das einfachste Beispiel eines Kraftwandlers ist der Hebel mit dem Hebelgesetz.

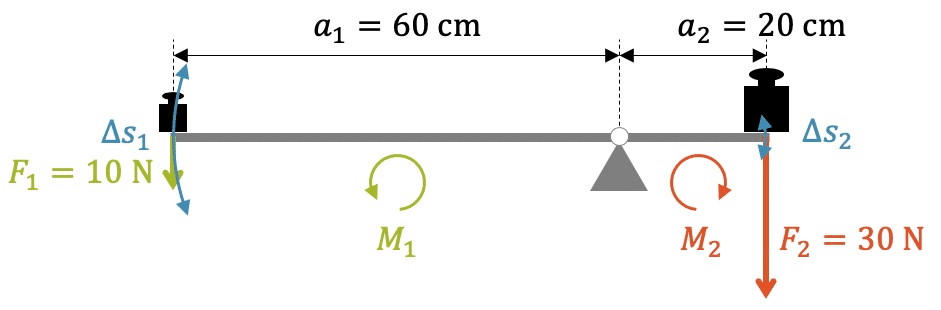
Die beiden ungleichen Gewichte sind auf einer Balkenwaage so aufgelegt, dass sie sich im Gleichgewicht befinden. Gemäss Hebelgesetz erzeugt die Kraft \(F_1\) über den dreimal grösseren Abstand \(a_1\) ein gleich grosses Drehmoment \(M_1\), wie die weit grössere Kraft \(F_2\) kombiniert mit dem kleineren Abstand \(a_2\).

Durch die ungleichen Abstände würden sich auch die beiden Enden verschieden stark bewegen. Die Kraft \(F_1\) befindet sich am langen Ende, das sich dreimal stärker bewegt und somit einen dreimal längeren Weg \(\Delta s_1\) zurücklegt. Am anderen Ende wirkt die die dreimal grössere Kraft \(F_2\), jedoch über einen dreimal kürzeren Weg.

Als Goldene Regel der Mechanik gilt das folgende Gesetz:

• Die kleinere Kraft wirkt über einen grösseren Weg (\(\Delta s_1\)) und
• die grössere Kraft wirkt über einen entsprechend kleineren Weg (\(\Delta s_2\)).

Eine kleine Kraft (\(F_1\)) (mit grossem Weg) wird in einem Kraftwandler in eine grössere Kraft (\(F_2\)) mit kurzem Weg umgewandelt.

Die Kräfte stehen im umgekehrten Verhältnis zu den Wegen (Strecken):

\[ \frac{F_1}{F_2} = \frac{\Delta s_2}{\Delta s_1} \]

Das kennen wir auch vom Fahrrad: Mit einem strengen Gang müssen wir viel Kraft aufbringen und die Pedalen drehen sich kaum. Mit einem leichteren Gang ist die Tretkraft sehr klein, dafür müssen wir unglaublich schnell treten, d.h. unsere Füssen legen einen langen Weg zurück.

Das Getriebe eines Autos ist zwar viel komplizierter und ist auch massiver gebaut. Es benutzt aber die gleiche Goldene Regel der Mechanik: viel Kraft bei kleinem Weg (untere Gänge) oder viel Weg bei kleiner Kraft (obere Gänge).

Eine Besonderheit ist das schöne Planetengetriebe, das z.B. in Windturbinen eingesetzt wird. Dieses Getriebe wandelt die sehr langsame Drehbewegung des Rotor in eine viel schnellere Drehbewegung um.

Für die Erzeugung der Wechselspannung im Generator ist die extrem langsame Drehbewegung bei ungeheuerlich grossen Kräften ungeeignet. Dank dem Getriebe dreht sich die Achse schneller und die Kräfte sind dafür um den gleichen Faktor schwächer.

Physikalische Arbeit bei Kraftwandlern

Wir können die Gleichung von vorhin auch umformen und erhalten die Gleichheit der physikalischen Arbeit der beiden Kräfte.

\[ \frac{F_1}{F_2} = \frac{\Delta s_2}{\Delta s_1} \]

Wir multiplizieren die Gleichung mit \(F_2\) und mit \(\Delta s_1\):

\[ W_1 = F_1 \cdot \Delta s_1 = F_2 \cdot \Delta s_2 = W_2 \]

Die Arbeit, die wir mit der einen Kraft am Kraftwandler verrichten, ist gleich gross, wie die Arbeit, die der Kraftwandler über die zweite Kraft verrichtet: Der Kraftwandler nimmt gleich viel Arbeit (Energie) auf, wie er wieder abgibt.

Wie wir gerade gesehen haben, gilt \(W_1 = W_2\), d.h. es wird gleich viel Arbeit über die Kraft \(F_1\) in den Kraftwandler gegeben, wie der Kraftwandler nachher über die Kraft \(F_1\) wieder abgibt:

\[ W_1 = F_1 \cdot \Delta s_1 = F_2 \cdot \Delta s_2 = W_2 \]

Die Goldene Regel der Mechanik könnten wir deshalb auch so übersetzen:

Eine Kraft kann in einem Kraftwandler zwar beliebig umgewandelt werden. Jedoch bleibt die physikalische Arbeit gleich, die der Kraftwandler aufgenommen hat und die der Kraftwandler wieder abgibt: Wir können die Kraft wandeln, nicht aber die Energie!

Im reibungslosen Fall nehmen Kraftwandler gleich viel Arbeit auf, wie sie wieder abgeben.

Flaschenzüge

Zu den Kraftwandlern gehören auch die Flaschenzüge, die die Menschen schon zur Römerzeit kannten.

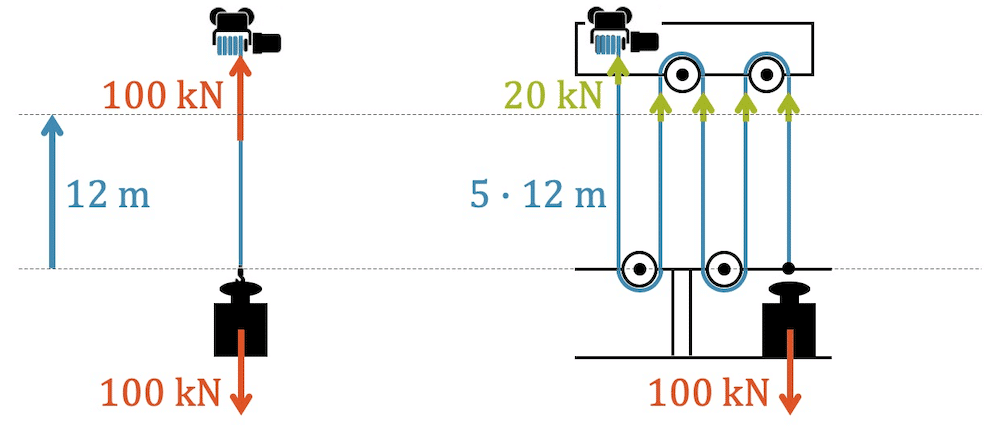
Mit Hilfe eines Flaschenzugs kann die limitierte Menschenkraft um Faktoren vergrössert werden. Dazu gleich ein Beispiel aus dem 16. Jahrhundert:

Das gleiche Prinzip finden wir noch heute bei vielen Kränen:

Auf Segelschiffen verwendete man Flaschenzüge, um die Segel anzuheben, aber auch um sie mit vielfach stärkeren Kräften zu spannen.

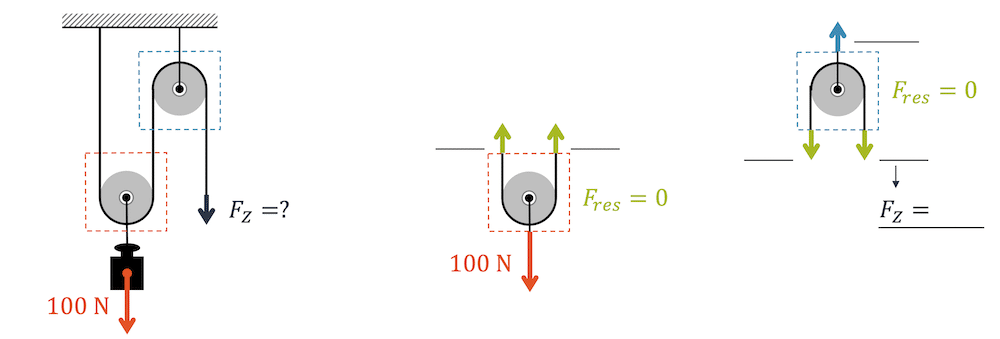
Der einfachste Flaschenzug hat nur gerade eine Rolle. Wir können einfach sehen, dass wegen des Flaschenzugs die doppelte Länge an Seil gezogen werden muss, um den gleichen Effekt beim Anheben zu erreichen.

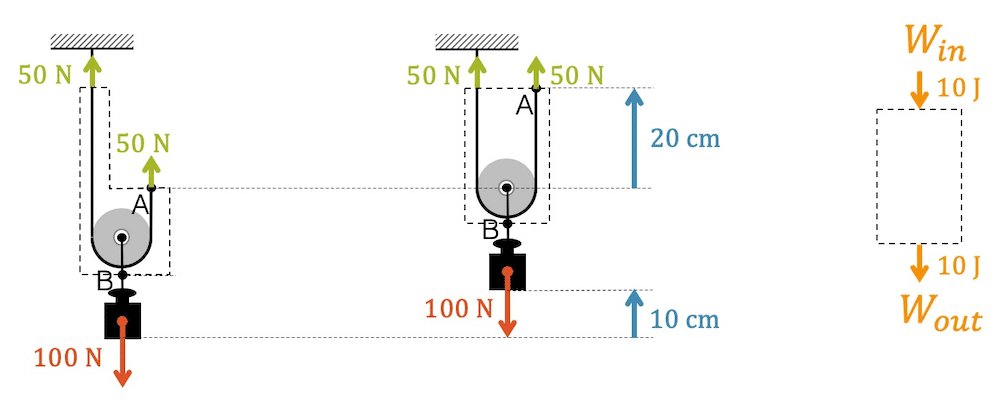
Aufgrund der Goldenen Regel der Mechanik wissen wir jetzt schon, dass doppelter Weg die halbe Kraft bedeutet, d.h. wir können mit dieser einen Rolle eine Last von 100 N mit einer Kraft von 50 N anheben – praktisch!

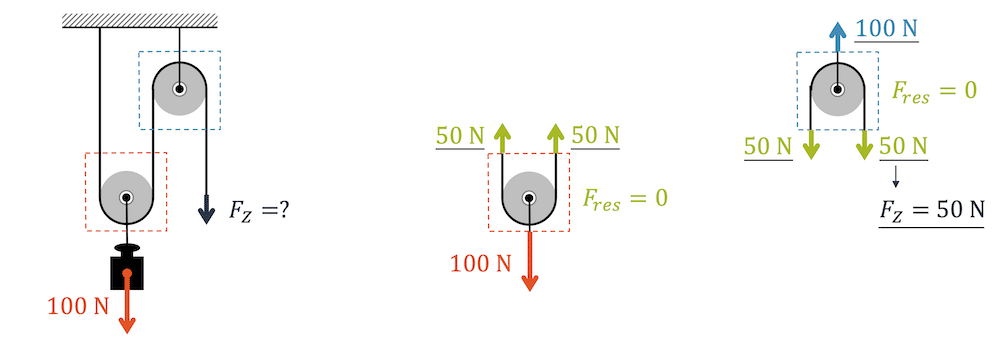
Für die Betrachtung der Kräfte werden wir im weiteren die Kräfte auf unser System (gestrichelte Linie) anschauen und annehmen, dass wir mit dem Ziehen kurz warten, d.h. es keine verwirrende Bewegung gibt (System in Ruhe, d.h. im Kräftegleichgewicht).

In der obigen Zeichnung sehen wir jetzt, dass wir zwei mal mit 50 N nach oben ziehen unten die Last mit 100 N nach unten zieht. Das System ist im Kräftegleichgewicht.

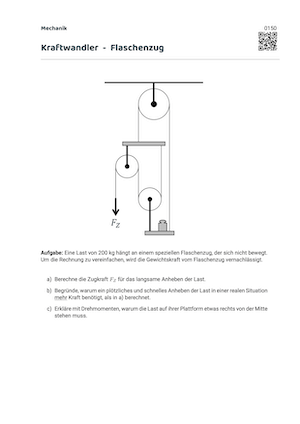
Beispiel

Bestimme in den folgenden Zeichnungen die Beträge der Kräfte für die einzelnen Teilsysteme eines Flaschenzugs mit zwei Rollen. Bestimme schliesslich die Zugkraft \(F_Z\), die für das Anheben der Last nötig ist.

Lösung

Im ersten Teilsystem (Mitte) haben wir die Last mit 100 N nach unten. Die beiden Kräfte nach oben sind unbekannt. Sie müssen aber gleich gross sein, denn sonst würde das Teilsystem ein resultierendes Drehmoment erleiden und kippen. Wir können deshalb auch hier folgern, dass die beiden Kräfte nach oben je 50 N betragen.

Im zweiten Teilsystem (rechts) übernehmen wir die eine Kraft von 50 N am rechten Seilstück des mittleren Teilsystems und übertragen sie auf das linke Seilstück des rechten Teilsystems. Die beiden Kräfte bilden im Sinne von Newtons Drittem Gesetz ein Kräftepaar. Sie repräsentieren die ein und dieselbe Kraft. Die andere Kraft nach unten muss auch 50 N betragen, weil sonst auch hier das zweite Teilsystem kippen würde. Wegen der beiden Kräfte von je 50 N nach unten, haben wir somit eine Kraft von 100 N nach oben. Die Zugkraft \(F_Z\) beträgt damit auch 50 N.

Beispiel

Ein Kranmotor, der eine Last von 100 kN anheben kann, soll mit einem kleineren Kranmotor ersetzt werden, kombiniert mit einem Flaschenzug mit 4 Rollen. Welche Last muss der neue Kranmotor tragen können? Welchen “Nachteil” müssen wir eingehen, wenn wir die Goldene Regel der Mechanik beachten?

Lösung

Links haben wir den alten Kranmotor, der die Last ohne Flaschenzug anhebt. Rechts ist ein Flaschenzug mit vier Rollen eingezeichnet. Die totale Zugkraft von 100 kN wird auf 5 Seile verteilt, so dass der neue Kranmotor nur noch ein Fünftel der Kraft erbringen muss, nämlich 20 kN. Dank der Goldenen Regel der Mechanik können wir eine Last (100 kN Gewichtskraft) mit einem Kran anheben, der aber nur 20 kN bringt. Der “Nachteil” ist, dass wir 5-mal mehr Drahtseil brauchen, denn der Kranmotor muss jetzt 60 m Seil aufwickeln, wenn er die Last um 12 m anheben will. Wir bezahlen die kleinere Kraft mit einem grösseren Weg. Beachte aber auch, dass das Drahtseil auch 5-fach schwächer und entsprechend dünner sein kann. Die Hubarbeit muss in beiden Fällen (mit oder ohne Flaschenzug) gleich sein, denn die Last muss in der höheren Position unbedingt immer die gleiche potenzielle Energie haben, unabhängig davon wie sie dorthin gekommen ist. \[ W = 100\,\mathrm{kN} \cdot 12\,\mathrm{m} = \frac{100}{5}\,\mathrm{kN} \cdot (5 \cdot 12\,\mathrm{m}) = 1.2\,\mathrm{MJ} \]