Inhalt
Videos
Zuerst schauen wir uns die Potenzfunktionen mit Exponenten 0, 1 und 2 an. Die grüne Linie wird beschrieben durch die nullte Potenz: \(f(x)=x^0=1\). Sie ist immer genau eins, egal welches \(x\) wir anschauen. Die blaue Linie ist definiert durch die erste Potenz: \(g(x)=x^1=x\). Es ist eine lineare Funktion mit Steigung eins und Achsabschnitt null. Schliesslich haben wir eine rote Parabel für die zweite Potenz: \(h(x)=x^2\).
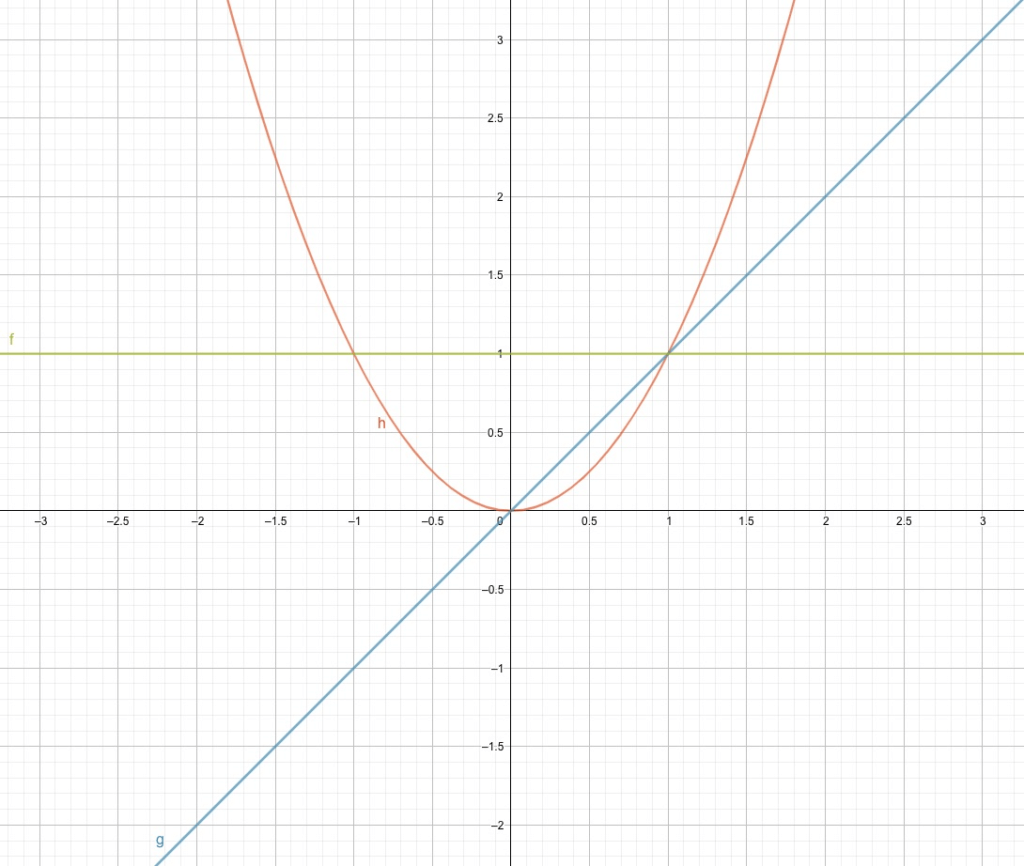
Die drei Verläufe sind auf den ersten Blick komplett verschieden. Es fällt uns aber auch auf, dass alle drei Verläufe einen gemeinsamen Punkt haben für \(x=1\). Wenn wir \(x=1\) einsetzen, kriegen wir immer eins als Resultat, was wir durch Einsetzen schnell überprüfen können:
\[ 1^0=1 \qquad 1^1=1 \qquad 1^2=1 \]
Dann sehen wir noch, dass die beiden Verläufe mit geraden Exponenten (0 und 2) sich ausschliesslich in der oberen Hälfte befinden, d.h. nur positive Werte ergeben. Die Parabel quadriert alle möglichen Werte von \(x\). Das Quadrieren macht selbst aus negativen \(x\)-Werten wieder ein positives Resultat, so dass die Parabel ausschliesslich positive Werte annimmt.
Die Potenz 1 ist die einzige Funktion, die auch negative Werte herausgibt. Das ist auch nicht erstaunlich, da die Potenz 1 einfach das Vorzeichen von \(x\) weitergibt.
Schau dir jetzt die zweite Abbildung an mit den Verläufen der dritten, vierten und fünften Potenz. Wir sehen, dass die beiden ungeraden Exponenten wieder nach links unten negative Werte annehmen, während die vierte Potenz als gerader Exponent immer nur positiv bleibt. Wir sehen auch, dass der Punkt (1,1) wieder ein gemeinsamer Punkt ist, denn
\[ 1^3=1 \qquad 1^4=1 \qquad 1^5=1 \]
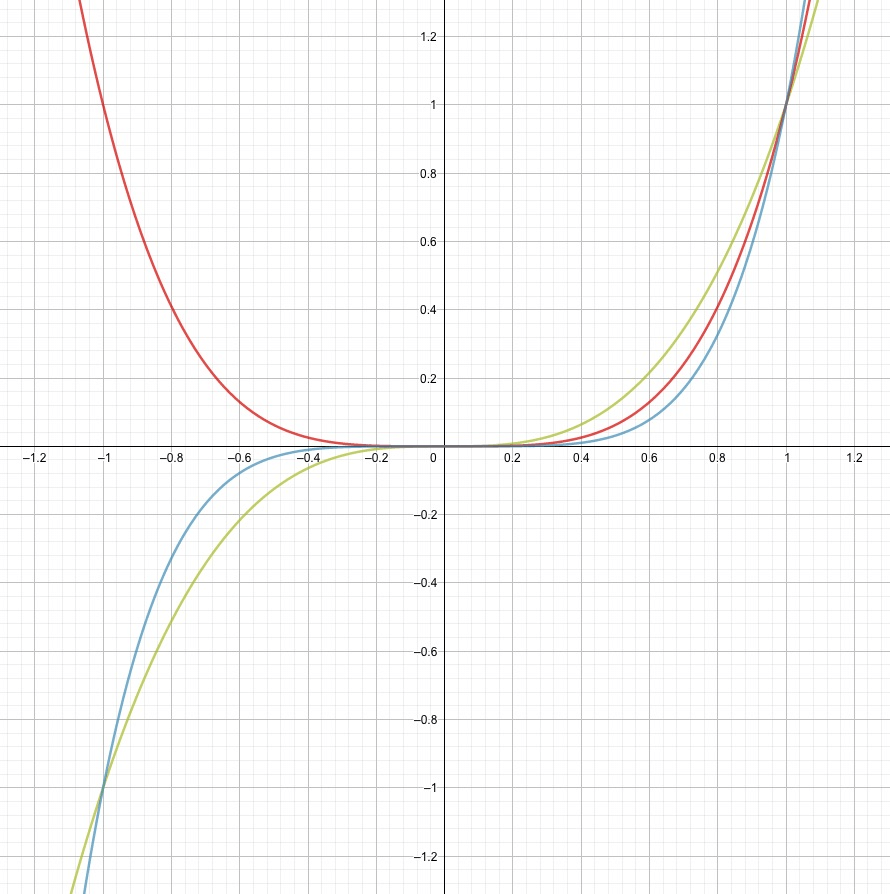
Wenn wir jetzt beim Nullpunkt (0,0) starten und langsam das \(x\) grösser werden lassen, dann sehen wir, dass die Verläufe länger bei kleinen Werten bleiben, je grösser der Exponent ist. Die fünfte Potenz (blau) bleibt länger unten und überholt die anderen Kurven erst ab (1,1). Die dritte Potenz nimmt als Erste Höhe an, steigt dann aber nach dem gemeinsamen Punkt (1,1) am langsamsten von den Dreien. Auch das können wir schnell verstehen. Für \(x<1\) (z.B. \(x=\frac{1}{2}\)) gilt:
\[ \Big (\frac{1}{2} \Big )^1 > \Big (\frac{1}{2} \Big )^2 > \Big (\frac{1}{2} \Big )^3 > \Big (\frac{1}{2} \Big )^4 > \Big (\frac{1}{2} \Big )^5 \]
Andererseits gilt für ein \(x>1\) (z.B. \(x=2\)) gerade das Umgekehrte:
\[ 2^1 \; < \; 2^2 \; < \; 2^3 \; < \; 2^4 \; < \; 2^5 \]
Potenzen \(x^n\) ergeben alle für \(x=1\) das Resultat 1, was den gemeinsamen Punkt \((1,1)\) erklärt.
Potenzen mit geraden Exponenten erzeugen ausschliesslich positive Resultate.
Potenzen mit ungeraden Exponenten geben das Vorzeichen von \(x\) weiter, d.h. für negative \(x\) ist die Potenz ebenfalls negativ, für positive \(x\) ist die Potenz positiv.
Beachte, dass es in der Mathematikwelt für den Spezialfall \(0^0\) keine Einigkeit gibt. Ist das Resultat jetzt auch 1 oder ist das Resultat undefiniert? Wir werden der Einfachheit halber sagen, dass alles hoch null eins ergibt, auch für null als Basis:
\[ 0^0 = 1 \]
Unter einer Potenzfunktion \(n\)-ter Ordnung verstehen wir eine Potenz mit einem ganzzahligen, positiven Exponenten \(n\):
\[ f(x) = x^n \]
Für den Exponenten \(n\) gilt: \(n \in \mathbb{N}\), womit auch gegeben ist, dass \(n>0\)
Potenzen mit ungeraden Exponenten
Für ungerade Exponenten \(n\) kriegen wir Verläufe, die zwar unterschiedlich aussehen, sonst aber viel gemeinsam haben.
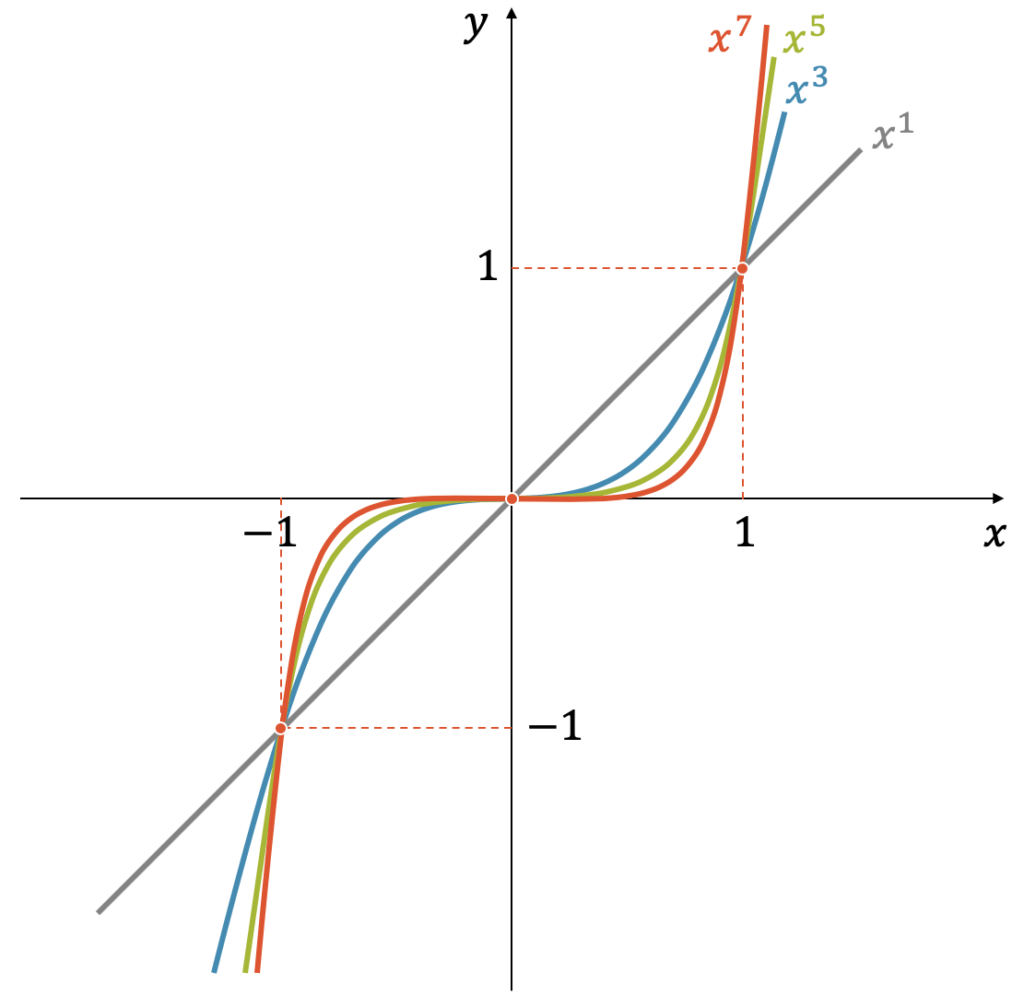
Nachfolgend sind ihre Eigenschaften aufgelistet:
- Die Funktionen verlaufen vom Quadranten unten links zum Quadranten oben rechts
- Ihre gemeinsamen Punkte sind: \((-1,-1)\) und \((1,1)\), unabhängig von \(n\)
- Je grösser \(n\), desto steiler verlaufen die Funktionen und desto grösser sind die Funktionswerte rechts von \((1,1)\)
- Zwischen dem Ursprung und dem Punkt \((1,1)\) werden die Funktionswerte mit grösserem \(n\) immer kleiner
- Der Wechsel der Steigung vor dem Punkt \((1,1)\) ist grösser, je grösser \(n\). Für den kleinsten Exponenten \(n=1\) gibt es gar keine Änderung der Steigung
Potenzen mit geraden Exponenten
Vieles ist bei den Potenzen mit geraden Exponenten \(n\) gleich, wie bei den Potenzen mit ungeraden Exponenten. Der augenfälligste Unterschied ist jedoch der Verlauf für negative \(x\)-Werte. Sie sind im Quadranten oben links, so dass wir sagen können, dass Potenzfunktionen mit geraden Exponenten nur positive Funktionswerte haben.
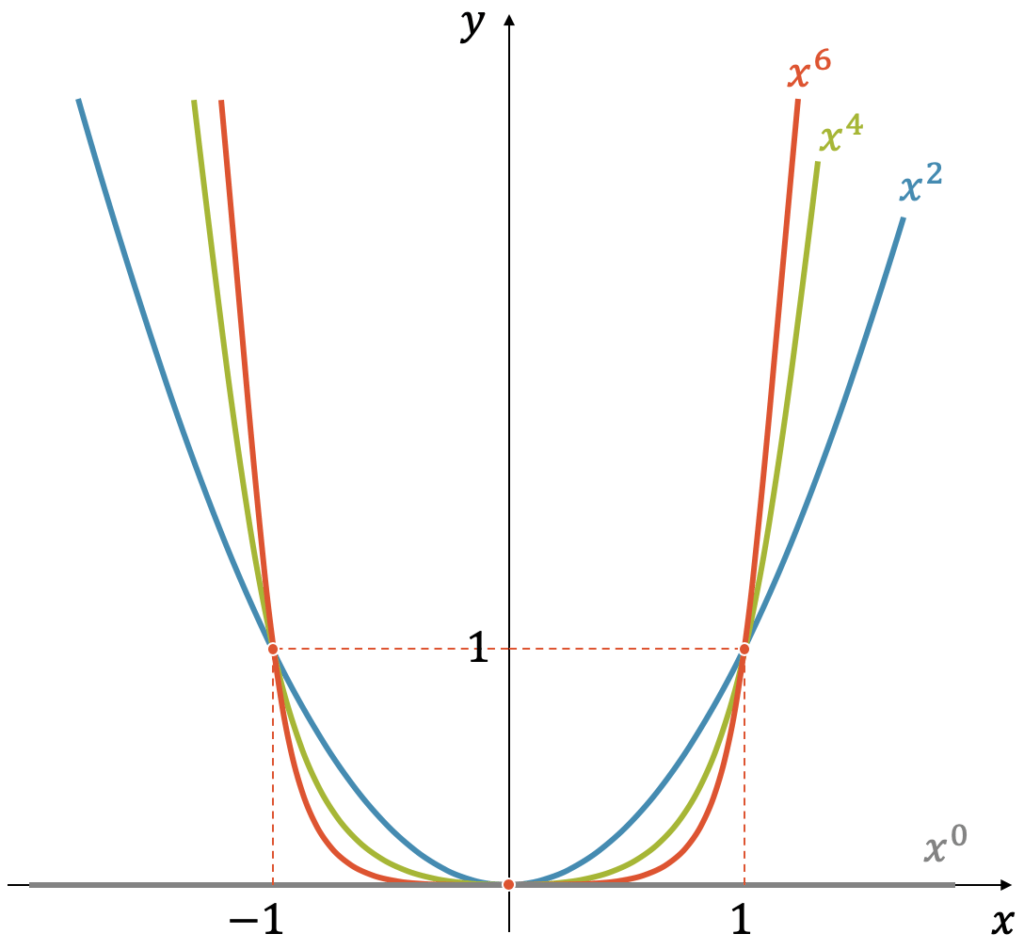
Nachfolgend sind ihre Eigenschaften aufgelistet:
- Die Funktionen verlaufen vom Quadranten oben links zum Quadranten oben rechts, d.h. die Funktionswerte sind immer positiv
- Ihre gemeinsamen Punkte sind: \((-1,1)\) und \((1,1)\), unabhängig von \(n\)
- Je grösser \(n\), desto steiler verlaufen die Funktionen und desto grösser sind die Funktionswerte rechts von \((1,1)\)
- Zwischen dem Ursprung und dem Punkt \((1,1)\) werden die Funktionswerte mit grösserem \(n\) immer kleiner
- Der Wechsel der Steigung vor dem Punkt \((1,1)\) ist grösser, je grösser \(n\).
Beispiel
Bestimme die Funktionsgleichung für den Verlauf im folgenden Diagramm:
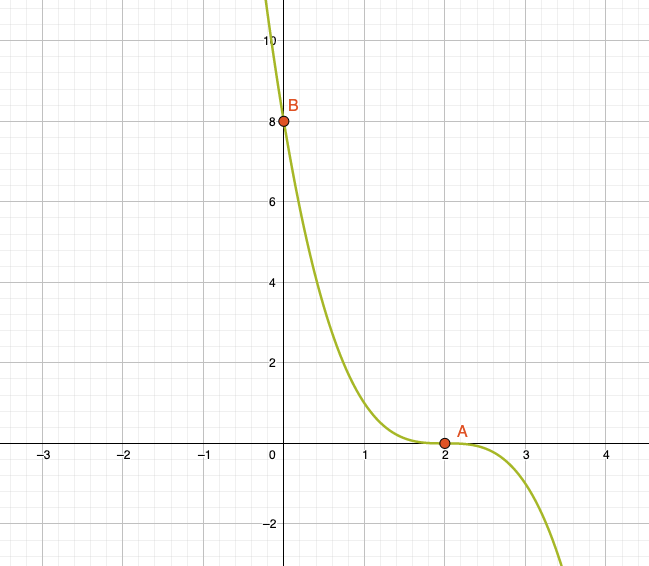
Als Erstes sehen wir, dass der Verlauf von oben links nach unten rechts verläuft. Einen solchen Verlauf kennen wir eigentlich nicht. Er entspricht aber dem Verlauf einer Potenzfunktion mit ungeradem Vorzeichen, wenn sie mit einem negativen Vorzeichen multipliziert wird, d.h. wenn die ganze Funktion gegenüber der \(x\)-Achse gespiegelt wird.
Dann fällt uns noch auf, dass der Graph nicht durch den Ursprung geht, sondern durch \(A(2,0)\). Scheinbar wurde der Graph um 2 Einheiten nach rechts verschoben worden, d.h. statt \(x\) schreiben wir \((x-2)\).
Schliesslich haben wir den Punkt \(B(0,8)\) als Information. Wenn wir den folgenden Ansatz machen, erhalten wir den Exponenten \(n=3\):
\[ -(0-2)^n = 8 \quad \rightarrow \quad n = 3 \]
Wir erhalten also folgende Funktionsgleichung:
\[ \underline{f(x) = -(x-2)^3} \]
Sie geht definitiv durch die beiden Punkte \(A\) und \(B\), denn \(\;-(2-2)^3=0\;\) und \(\;-(0-2)^3=8 \;\). Beim genaueren Hinschauen, erkennen wir, dass die Kurve beispielsweise durch den Punkt \((1,1)\) verläuft. Tatsächlich stimmt unsere Funktionsgleichung auch hier überein: \(\;-(1-2)^3=1\;\).
Aufgabensammlung
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.
Inhalt







Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.