Inhalt
Das Wichtigste in Kürze
Das dreidimensionale Koordinatensystem wird meistens wie folgt gezeichnet:
-
-
- \((x,y)\)-Ebene liegt gedreht vor uns
- Die Zeichenebene ist neu die \((y,z)\)-Ebene
- Die \(z\)-Achse übernimmt die Rolle der “Höhe”
- Die \(x\)-Achse zeigt perspektivisch aus der Zeichenebene heraus (Parallelperspektive mit 45°-Winkel, verkürzte Skala)
-
Punkte können eindeutig eingezeichnet werden, jedoch kann von einem Punkt nicht mehr eindeutig bestimmt werden, welche Koordinaten er hat.
Videos
Für die räumliche Vektorgeometrie brauchen wir eine Möglichkeit, Vektoren, Geraden, Punkte usw. im Raum darzustellen. Dazu benutzen wir ein Koordinatensystem mit den drei Dimensionen \(x\), \(y\) und \(z\). Es ist üblich dafür die Parallelperspektive zu verwenden. Die Zentralperspektive würde zwar besser aussehen, wäre aber viel zu aufwendig. Auf der \(x\)-Achse werden die Abstände auf der Skala etwas verkürzt im Vergleich zu den Abständen auf der \(y\)- und \(z\)-Achse.
Die \(y\)- und die \(z\)-Koordinaten legen wir neu in die Zeichenebene. Das ist am Anfang etwas gewöhnungsbedürftig, denn hier sind wir gewohnt die \(x\)- und die \(y\)-Koordinate zu haben. Vor allem zeigt die \(y\)-Achse jetzt plötzlich horizontal nach rechts!
Die \(x\)-Koordinate haben wir nach vorne gelegt, also eigentlich räumlich aus der Zeichenebene heraus. Für die perspektivische Darstellung nehmen wir einen 45°-Winkel, weil der am einfachsten ist. Wir sehen jetzt, dass die \((x,y)\)-Ebene unten liegt (grün eingefärbt). Wir schauen irgendwie von oben darauf.
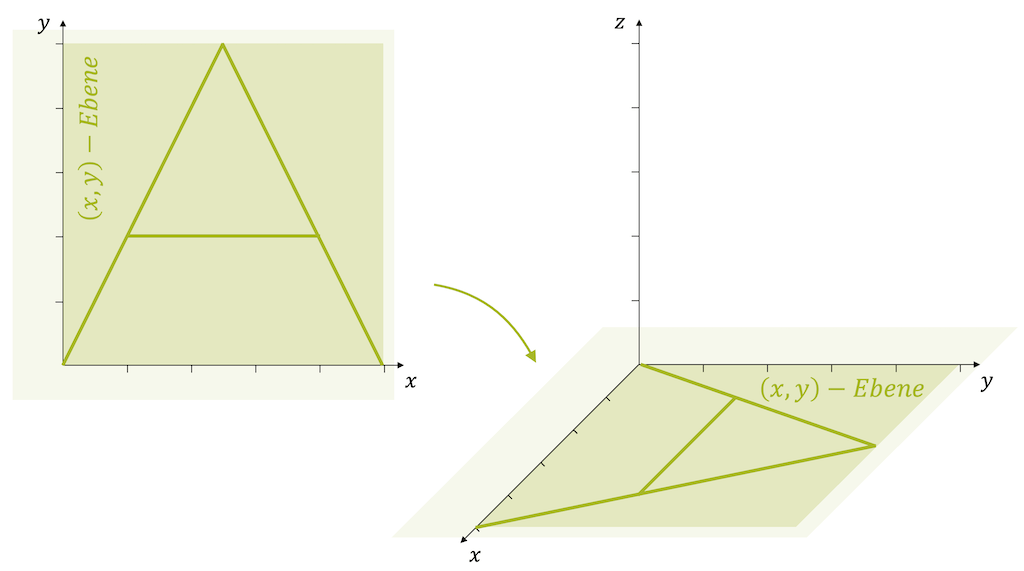
Das dreidimensionale Koordinatensystem wird meistens wie folgt gezeichnet:
- \((x,y)\)-Ebene liegt gedreht vor uns
- Die Zeichenebene ist neu die \((y,z)\)-Ebene
- Die \(z\)-Achse übernimmt die Rolle der “Höhe”
- Die \(x\)-Achse zeigt perspektivisch aus der Zeichenebene heraus (Parallelperspektive mit 45°-Winkel, verkürzte Skala)
Punkte können eindeutig eingezeichnet werden, jedoch kann von einem Punkt nicht mehr eindeutig bestimmt werden, welche Koordinaten er hat.
Beispiel
Zeichne die folgenden vier Punkte in ein dreidimensionales Koordinatensystem ein.
\[ A(2,-3,4), \quad B(3,2,-1), \quad C(-4-2,0) \quad D(0,0,2) \]
Zeichne anschliessend die Vektoren \(\overrightarrow{OA}\) und \(\overrightarrow{CD}\).
Mini-Test
Um Zugang zum Mini-Test zu kriegen,
musst du vollwertiges Mitglied im Hacker-Club sein.
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.
Inhalt



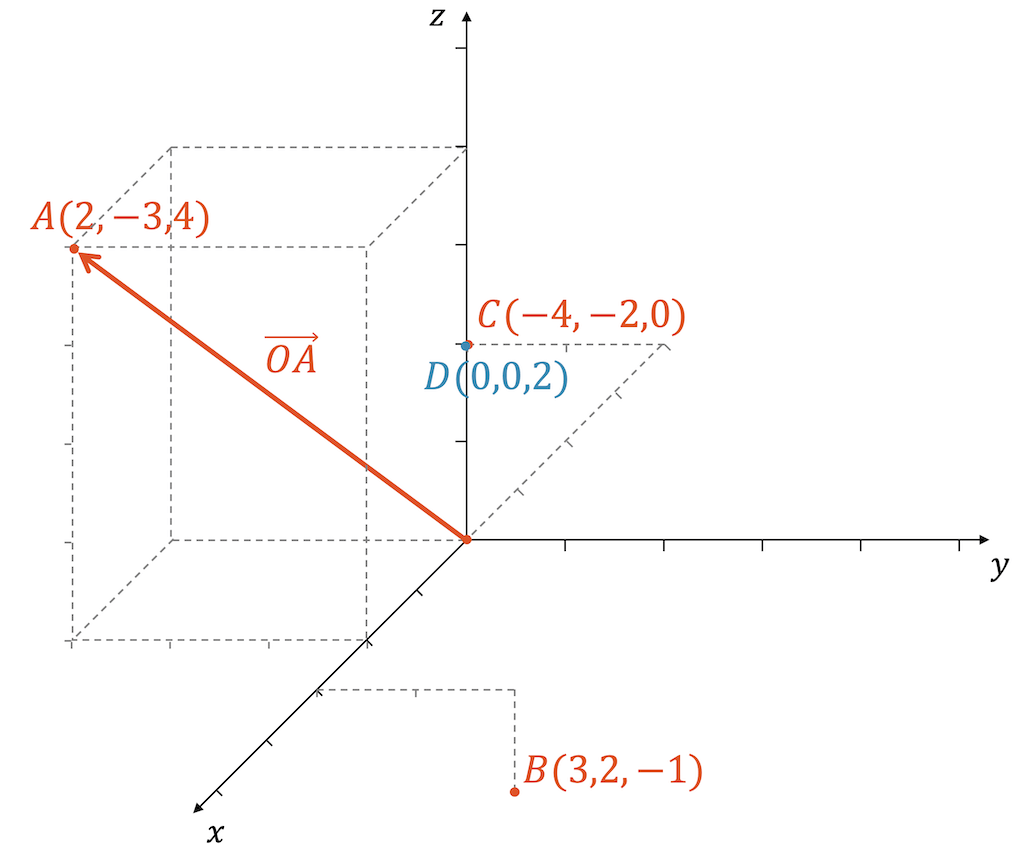




Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.