Inhalt
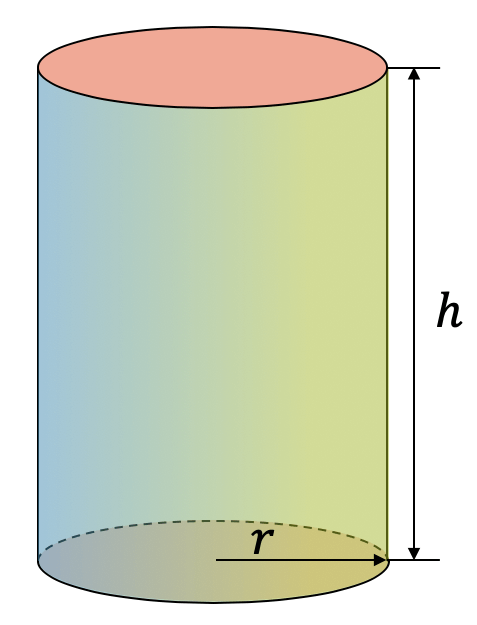
Der Zylinder hat einen Kreis als Grundfläche. Er kann, wie das Prisma, gerade oder scheif sein. Auch hier sind, gemäss dem Prinzip von Cavalieri, die Grundfläche und die Höhe entscheidend. Wie beim Prisma, ist auch hier das Volumen gleich dem Produkt von Grundfläche mal Höhe, denn eigentlich ist der Zylinder ein Prisma mit der Grundfläche eines \(n\)-Ecks mit \(n \rightarrow \infty\).
\[ V = G \cdot h = \pi r^2 h \]
Bevor wir die Oberfläche berechnen, werden wir zuerst das Netz eines Zylinders zeichnen. Die Mantelfläche ist beim geraden Zylinder ein Rechteck. Die eine Seite (Nummer 3 im Netz) ist keine Kante und deshalb mit einer Klammer versehen. An diesem Ort kommen aber die beiden Enden der Mantelfläche zusammen. Dieses Ende hat die Höhe \(h\) des Zylinders.
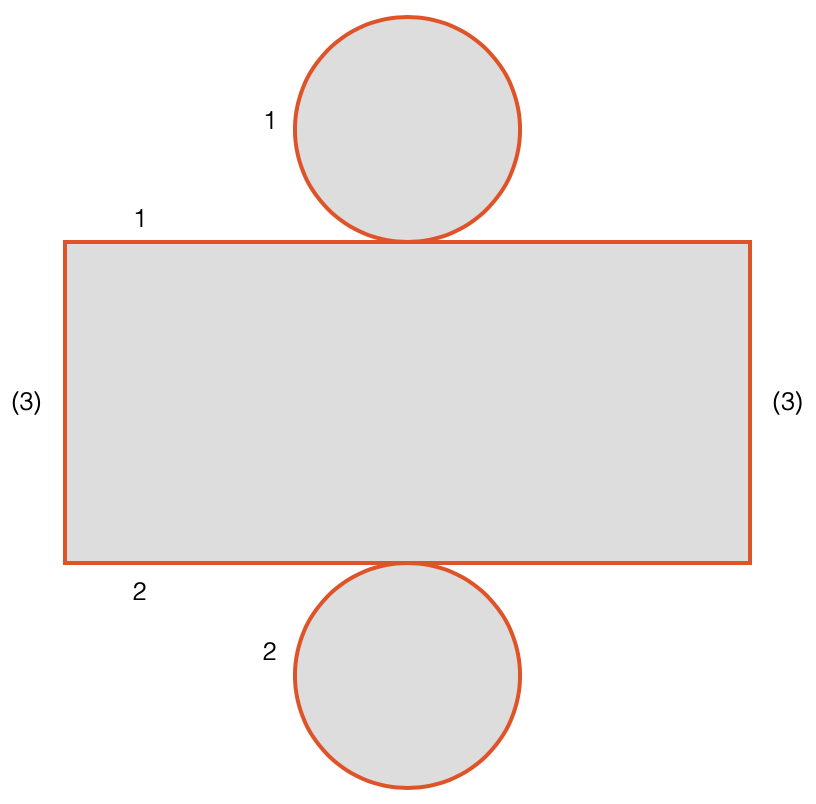
Die beiden Kanten 1 und 2 entsprechen dem Ort, wo die Rechteckfläche auf die Kreisfläche trifft. Die gemeinsame Kante entspricht dem Kreisumfang, d.h. \(U = \pi r\).
Für die Rechteckfläche haben wir deshalb:
\[ A_3 = h \cdot (2 \pi r) = 2 \pi r h \]
Nun addieren wir die beiden Kreisflächen \(A_1=A_2=\pi r^2\). Für die Oberfläche \(O\) des geraden Zylinders erhalten wir so:
\[ O = A_1 + A_2 + A_3 = 2\pi r^2 + 2 \pi r h = 2 \pi r \cdot (r + h) \]
Der Zylinder kann gerade oder schief sein. Er hat einen Kreis als Grundfläche und kann, analog zu einem \(n\)-Eck-Prisma berechnet werden, d.h. das Volumen entspricht der Grundfläche mal der Höhe:
\[ V = \pi r^2 h \]
Die Oberfläche des geraden Zylinders entspricht den beiden Kreisflächen und der rechteckigen Mantelfläche, deren eine Seite dem Kreisumfang entspricht:
\[ O = 2\pi r^2 + 2 \pi r h \]
Beispiel
Finde das Netz für einen Zylinderstumpf, der durch einen 45°-Schnitt durch einen Zylinder entsteht.
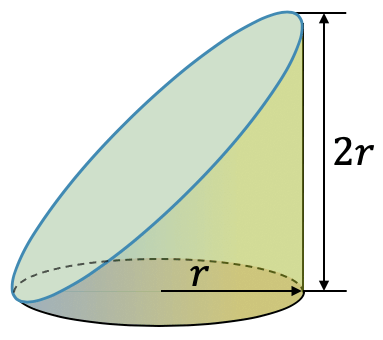
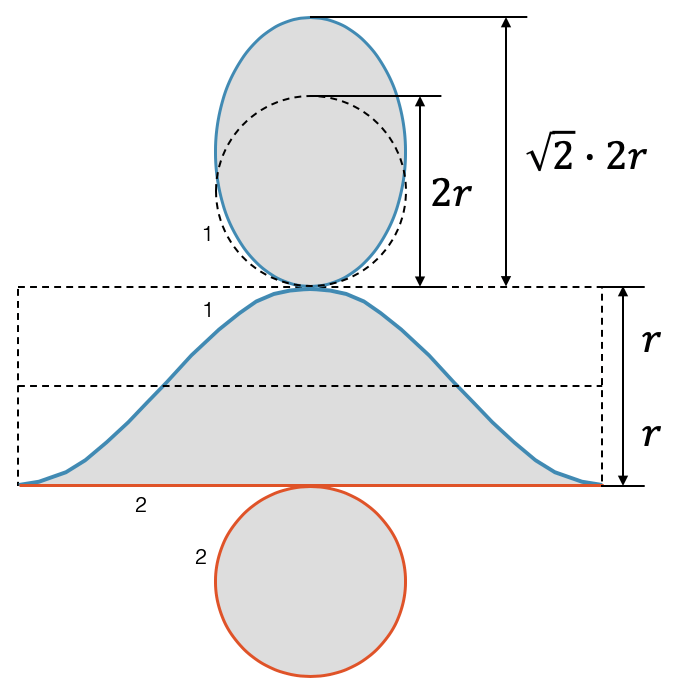
Wir starten mit dem Netz des Zylinders mit der Höhe \(2r\). Im ursprünglichen Rechteck der Mantelfläche starten wir ganz links, wo der Zylinderstumpf die Höhe null hat. Dann muss die Höhe leicht ansteigen. Nach einer Viertelumdrehung sollten wir auf halber Höhe sein, d.h. auf Höhe \(r\). Nach einer halben Umdrehung haben wir die ganze Höhe \(2r\) erreicht, nach drei Viertel einer Umdrehung sind wir wieder bei \(r\).
Da die Höhe eine Funktion der “Umdrehung” ist und wir zwischen 0 und \(2r\) schwanken, liegt es nahe, dass es sich hier um eine trigonometrische Funktion handelt. Wenn wir die Mittellinie der Mantelfläche nehmen, dann starten wir bei \(-r\) und gehen bis zu \(r\) hinauf und dann wieder runter auf \(-r\). Das entspricht einem negativen Kosinus:
\[ h(\alpha) = r – r \cdot cos(\alpha) \]
| \(\alpha\) | 0° | 90° | 180° | 270° | 360° |
| \(r – r \cdot cos(\alpha)\) | \(r-r \cdot 1 =0\) | \(r-r \cdot 0 =r\) | \(r-r \cdot (-1) =2r\) | \(r-r \cdot 0 =r\) | \(r-r \cdot 1 =0\) |
Jetzt brauchen wir noch die Ellipse für die Schnittfläche. In der Breite ist sie immer noch \(2r\). In der Länge ist sie jetzt aber um den Faktor \(\sqrt{2}\) gestreckt, denn wir schneiden mit 45° und das bedeutet, dass die ursprüngliche Breite von \(2r\) jetzt um den \(\sqrt{2}\) gestreckt worden ist, genau wie die Quadratsseite von \(s\) zu \(\sqrt{2}s\) wird, wenn wir die Diagonale des Quadrats nehmen.
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.
Inhalt






Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.