Inhalt
Videos
Pythagoras von Samos (ca. 570 v. Chr. – 510 v. Chr.) war ein antiker griechischer Philosoph und Gründer einer einflussreichen religiös-philosophischen Bewegung. Vieles zu seiner Person ist umstritten oder Stoff von Legenden. Er gilt aber als einer der Begründer der Geometrie bzw. Mathematik.
Der griechische Mathematiker Euklid von Alexandria lebte wahrscheinlich im 3. Jahrhundert v. Chr. in Alexandria und beschrieb die Satzgruppe des Pythagoras, die drei Sätze für rechtwinklige Dreiecke umfasst:
- Satz des Pythagoras
- Höhensatz
- Kathetensatz
Der erste dieser drei Sätze ist der Satz des Pythagoras. Er ist wohl einer der meist verwendeten Sätze der Geometrie:
Satz des Pythagoras: Die Summe der Quadrate der beiden Katheten \(a\) und \(b\) ist gleich dem Quadrat der Hypotenuse \(c\):
\[a^2 + b^2 = c^2 \]
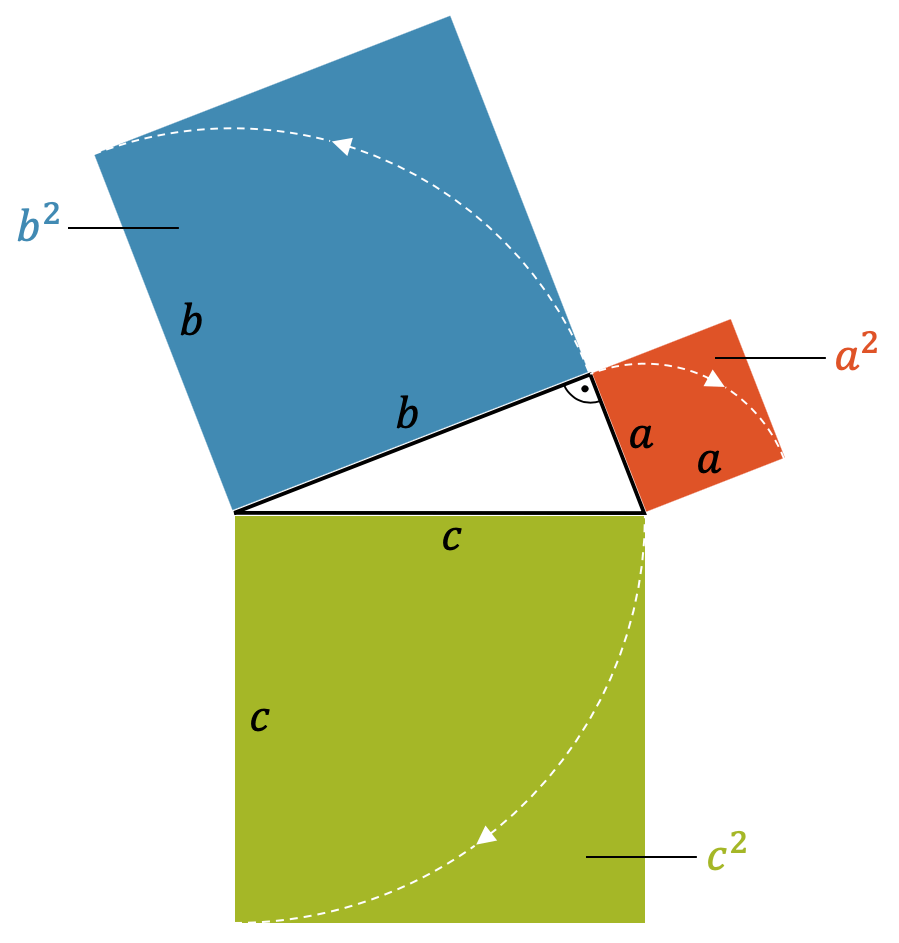
Wir können den Satz des Pythagoras auch graphisch darstellen, indem wir um das Dreieck herum die einzelnen Seiten mit dem Zirkel umklappen und so jeweils ein Quadrat bilden mit der Fläche \(a^2\) (rot), \(b^2\) (blau) bzw. \(c^2\) (grün). Der Satz des Pythagoras besagt nun, dass die Fläche des roten und blauen Quadrats zusammen die Fläche des grünen Quadrats ergeben.
Beweis
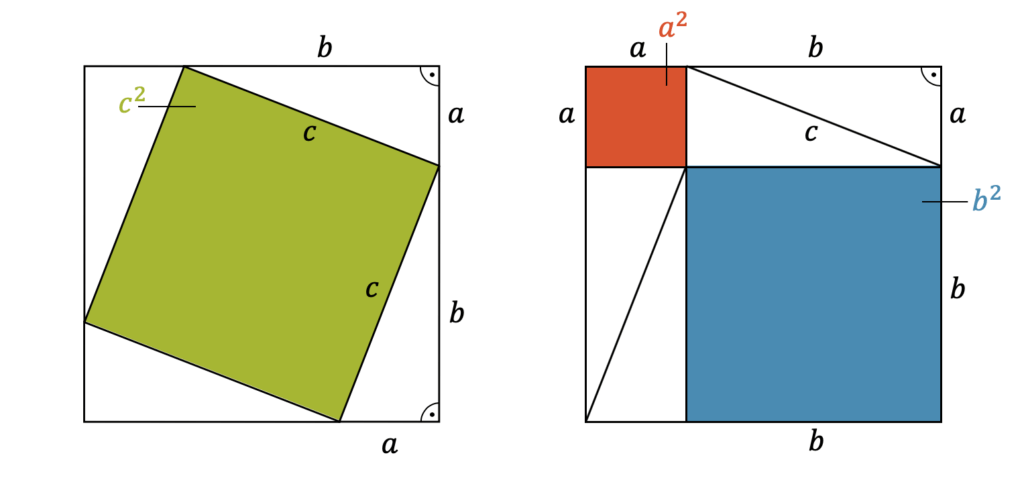
Wir können den Satz des Pythagoras am besten graphisch beweisen. Dazu nehmen wir vier gleiche rechtwinklige Dreiecke mit den beiden Katheten \(a\), \(b\) und der Hypotenuse \(c\). Wir können dieses Dreiecke so anordnen, dass sie ein Quadrat mit der Seitenlänge \((a+b)\) erzeugen. Zwischen den Dreiecken entsteht ein Loch der Fläche \(c^2\).
Wenn wir jetzt das grosse Quadrat behalten, aber die vier Dreiecke etwas anders platzieren, erhalten wir zwei quadratische Löcher mit den Flächen \(a^2\) und \(b^2\). Da wir das gleich grosse Quadrat mit den Seiten \((a+b)\) beibehalten haben, wurde das ursprüngliche Loch der Fläche \(c^2\) einfach in zwei separate Quadratflächen umgewandelt. Sie müssen zusammen aber die gleiche Fläche ausmachen wie \(c^2\). Deshalb muss gelten…
\[a^2 + b^2 = c^2 \]
…womit der Satz des Pythagoras bewiesen ist.
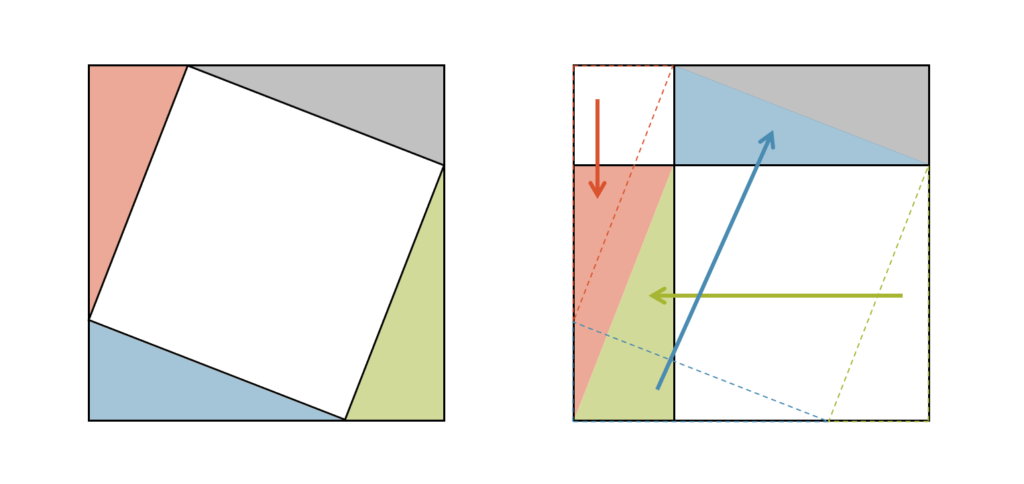
Wir können den Satz des Pythagoras auch mit ein bisschen Algebra beweisen. Das grosse Quadrat hat die Fläche \((a+b)^2\). Mit Hilfe der binomischen Formel erhalten wir:
\[(a+b)^2 = a^2 + 2ab + b^2 \]
Jetzt ziehen wir das Loch ab und erhalten so die 4-fache Fläche \(A\) der rechtwinkligen Dreiecke:
\[a^2 + 2ab + b^2 – c^2 = 4 \cdot A \]
Wenn wir die beiden Katheten des rechtwinkligen Dreiecks multiplizieren (\(a \cdot b\)) erhalten wir ein Rechteck mit der doppelten Fläche des Dreiecks. Die Diagonale im Rechteck teilt es in zwei gleich grosse Dreiecke mit der Fläche \(A\).
\[A = \frac{1}{2}ab \]
Wir setzen dies oben ein, subtrahieren dann \(2ab\) und erhalten so
\[a^2 + 2ab + b^2 – c^2 = 4 \cdot \frac{1}{2}ab = 2ab \]
\[ \require{cancel} a^2 + \cancel{2ab} + b^2 – c^2 = \cancel{2ab} \]
\[a^2 + b^2 – c^2 = 0 \quad \rightarrow \quad a^2 + b^2 = c^2 \]
Anwendungen in rechtwinkligen Dreiecken
Auch wenn wir kein rechtwinkliges Dreieck haben, lassen sich z.B. durch Einführen einer Höhe immer ein oder zwei rechtwinklige Dreiecke finden, für die der Satz des Pythagoras angewendet werden kann.
Beispiel
Bestimme die Höhe \(h\) in einem gleichseitigen Dreieck.
Wir machen eine kleine Skizze eines gleichseitigen Dreiecks mit den Seiten \(s\) und den Winkeln von \(60°\). Wir zeichnen auch die Höhe \(h\) ein.
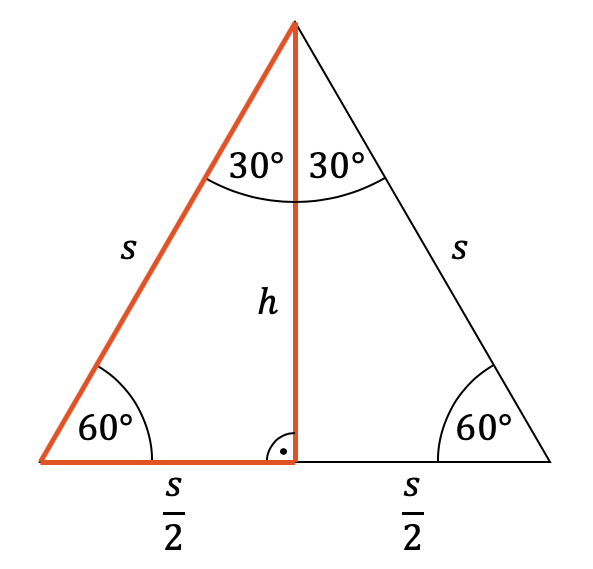
Mit der Höhe entstehen zwei rechtwinklige Dreiecke mit den beiden Katheten \(\frac{s}{2}\) und \(h\) und der Hypotenuse \(s\). Wir können für dieses rechtwinklige Dreieck den Satz des Pythagoras einsetzen:
\[h^2 + \Big (\frac{s}{2} \Big) ^2 = s^2 \]
Da wir \(h\) bestimmen möchten, subtrahieren wir in der Gleichung den Bruch im Quadrat.
\[h^2 = s^2 – \Big (\frac{s}{2} \Big) ^2 = s^2 – \frac{s^2}{4} = (1-\frac{1}{4})\cdot s^2 = \frac{3}{4}s^2 \]
Jetzt ziehen auf beiden Seiten der Gleichung die Wurzel
\[h = \sqrt{\Big(\frac{3}{4}s^2\Big)} = \frac{\sqrt{3}}{2}s \]
Beispiel
Berechne die Diagonale \(d\) eines Quadrats mit Seitenlänge \(s\).
Wir machen als erstes eine kleine Skizze des Quadrats mit Seitenlänge \(s\) und zeichnen die Diagonale ein.
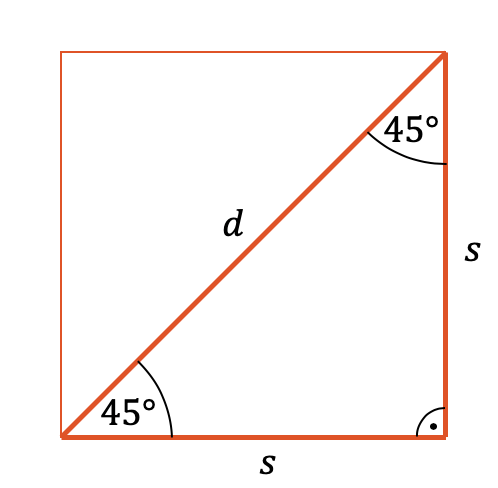
Jetzt sehen wir natürlich das rechtwinklige Dreieck, für welches wir den Pythagoras anwenden können. Es hat die beiden gleichen Katheten \(s\) und die Diagonale \(d\) bildet die Hypotenuse. Der Satz des Pythagoras lautet deshalb:
\[s^2 + s^2 = d^2 \]
Wir vertauschen die beiden Seiten, addieren die \(s^2\) und ziehen die Wurzel auf beiden Seiten der Gleichung:
\[d^2 = 2s^2 \quad \rightarrow \quad d = \sqrt{2} s \]
Anwendung im Koordinatensystem (zweidimensional)
Der Satz von Pythagoras ist ein sehr nützliches Werkzeug für die Berechnung von Distanzen zweier Punkte in einem rechtwinkligen Koordinatensystem.
Beispiel
Berechne den Abstand \(a\) zwischen den Punkten A(5,1) und B(2,3).
Wir zeichnen ein Koordinatensystem und tragen die beiden Punkte A und B ein. Der Abstand \(a\) ist die direkte (gerade) Verbindung zwischen den beiden Punkten.
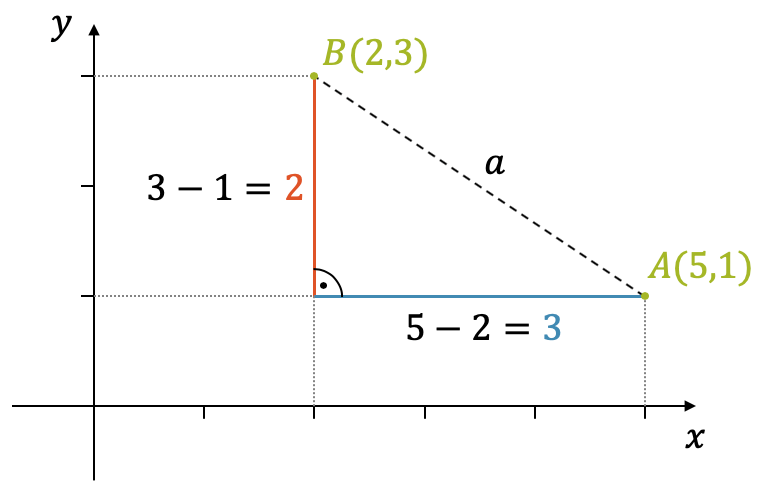
Wir sehen sofort, dass sich ein rechtwinkliges Dreieck bilden lässt: Die horizontale Kathete ist der horizontale Abstand der beiden \(x\)-Koordinaten: \(5-2=3\). Vertikal sind die beiden Punkte \(3-1=2\) auseinander.
Mit dem Satz des Pythagoras berechnen wir so die Hypotenuse \(a\):
\[a^2 = 3^2 + 2^2 = 9+4 = 13 \]
Wir erhalten somit einen Abstand \(a=\sqrt{13}\)
Der Abstand \(a\) zwischen zwei Punkten A und B kann mit Hilfe ihrer Koordinaten bestimmt werden. Im zweidimensionalen Koordinatensystem kann ein rechtwinkliges Dreieck bestimmt werden. Die eine Kathete ist durch die Differenz der \(x\)-Koordinaten, die andere Kathete durch die Differenz der \(y\)-Koordinaten gegeben:
\[a=\sqrt{(A_x-B_x)^2 + (A_y-B_y)^2}\]
Anwendung im Koordinatensystem (dreidimensional)
Wenn wir Abstände zwischen zwei Punkten im Raum berechnen müssen, können wir dies auch mit dem Satz des Pythagoras tun. Allerdings geht das nicht in einem Schritt, sondern wir müssen zwei rechtwinklige Dreiecke aufstellen.
Wir schauen uns das an einem Beispiel an: Gesucht ist der Raumabstand \(d\) zwischen den Punkten A(0,4,0) und B(3,0,5).
Als Erstes zeichnen wir ein dreidimensionales Koordinatensystem mit den drei Achsen \(x\), \(y\) und \(z\). Es ist üblich, die \(x\)-Achse nach vorne zu nehmen, d.h. aus der Zeichenebene heraus. Die \(y\)-Achse zeigt jetzt nach rechts und die Achse für die Vertikale ist die \(z\)-Achse. Natürlich kann das Koordinatensystem auch anders gedreht und dargestellt werden. Diese Darstellung ist aber die üblichste Ansicht, mit welcher man anfängt.
Jetzt können wir die beiden Punkte A und B einzeichnen. A liegt auf der \(y\)-Achse. B liegt auf der \(x,z\)-Ebene. Gesucht ist die gerade Verbindung \(d\) zwischen den beiden.
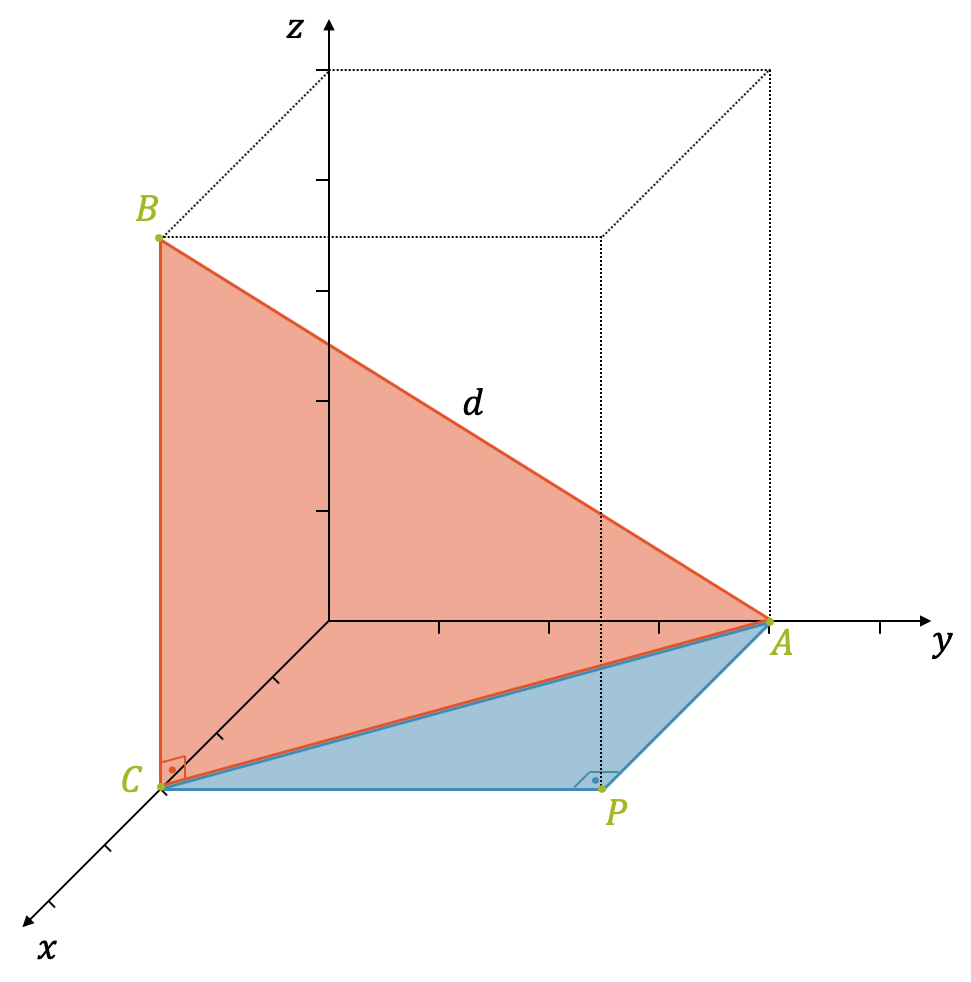
Als Erstes suchen wir ein rechtwinkliges Dreieck, so dass wir den Satz des Pythagoras anwenden können. Das rote Dreieck hat einen rechten Winkel beim Punkt C, denn die Strecke [AC] liegt in der \(x,y\)-Ebene, d.h. auf der “Bodenebene”. Die andere Strecke [CB] ist parallel zur \(z\)-Achse und ist somit senkrecht zur “Bodenebene”. Das rote Dreieck ABC ist deshalb ein rechtwinkliges Dreieck mit den beiden Katheten [AC] und [BC] und der Hypotenuse \(d\). Wenn wir also die Längen der Strecken \(\overline{AC}\) und \(\overline{BC}\) haben, können wir \(d\) mit dem Satz des Pythagoras bestimmen:
\[\overline{BC}\,^2 + \overline{AC}\,^2 = d^2 \]
Die Länge \(\overline{BC}\) kann einfach aus den \(z\)-Koordinaten der Punkte B und C erhalten werden:
\[\overline{BC} = B_z – C_z = 5 – 0 = 5 \]
Die Länge \(\overline{AC}\) kann nicht so direkt gefunden werden. Sie muss als Abstand zweier Punkte in einer \(x,y\)-Ebene bestimmt werden, d.h.
\[\overline{AC} = \sqrt{(A_x-C_x)^2 + (A_y-C_y)} \]
Wir können die Koordinaten direkt oben einsetzen oder uns dieses blaue rechtwinklige Dreieck in der \(x,y\)-Ebene aufzeichnen. Dazu stellen wir uns vor, wir würden über der \(x,y\)-Ebene schweben und würden senkrecht nach unten schauen, also gerae der \(z\)-Achse entgegengesetzt.
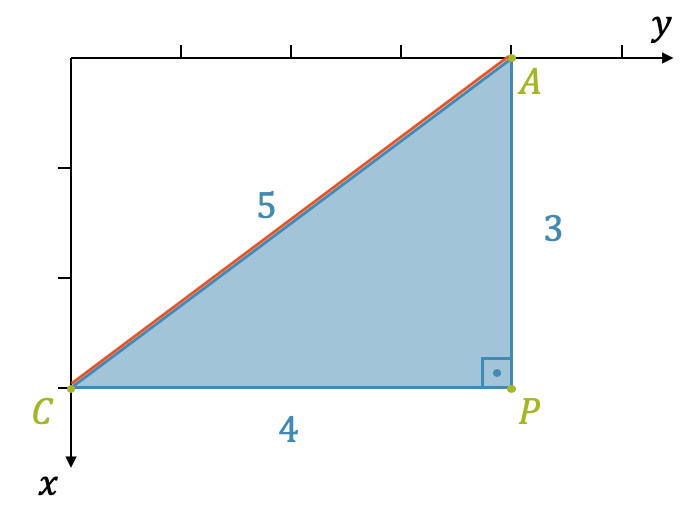
Jetzt sehen wir sehr schön, dass das blaue Dreieck zwei Katheten mit den Längen \(3\) und \(4\) hat, d.h. die Hypotenuse [AC] hat demzufolge die Länge: \(\sqrt{3^2+4^2}=5\).
Wir gehen zurück zum roten Dreieck. Die Längen der beiden Katheten [BC] und [AC] sind bekannt und wir können den Satz des Pythagoras anwenden. Zur Verdeutlichung zeichnen wir das rote Dreieck in seiner eigenen Ebene.
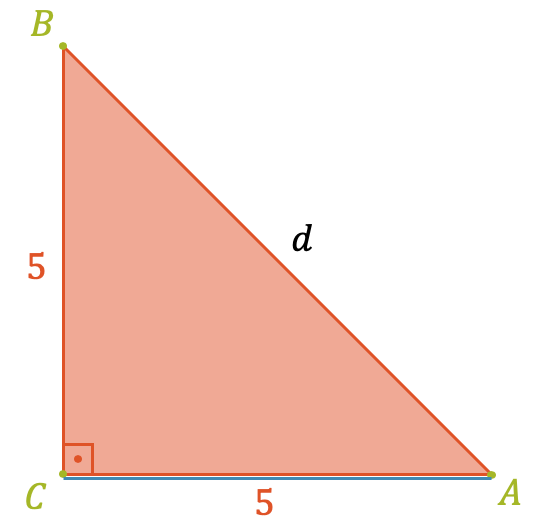
Beide Katheten haben die Länge \(5\) und somit ist der Winkel von \(d\) gegenüber der “Bodenebene” \(45°\). Es ist eine Diagonale eines Quadrats und wir schreiben einfach:
\[d = \sqrt{2}\cdot 5 \approx 7.07 \]
Das gleiche Resultat erhalten Sie natürlich auch mit dem Satz des Pythagoras: \(d = \sqrt{5^2 + 5^2} = \sqrt{2 \cdot 5^2}\)
Der Raumabstand \(a\) zwischen zwei Punkten A und B kann mit Hilfe ihrer Koordinaten bestimmt werden. Im dreidimensionalen Koordinatensystem werden zwei rechtwinklige Dreiecke gesucht und zwei Mal mit dem Satz des Pythagoras berechnet.
Allgemein gilt aber auch einfach:
\[a=\sqrt{(A_x-B_x)^2 + (A_y-B_y)^2 + (A_z-B_z)^2} \]
Aufgabensammlung
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.
Inhalt








Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.