Inhalt
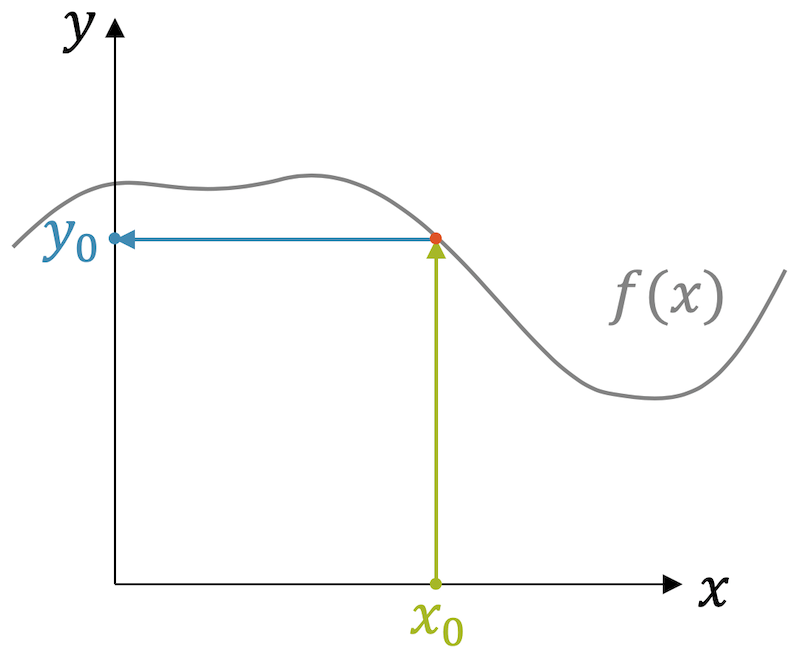
Die Funktion weist dem Wert \(x\) einen Funktionswert zu, den nennen wir \(f(x)\) und diesen weisen wir \(y\) zu. Im \(x,y\)-Koordinatensystem haben wir eine Zuordnung durch \(f\) von einem bestimmten Wert \(x_0\) auf den Wert \(y_0\):
\[ y_0 = f(x_0) \]
Wir können das für alle Werte von \(x\) wiederholen und erhalten dann eine Punkteschar mit den Koordinaten \((x_0,y_0)\), \((x_1,y_1)\), \((x_2,y_2)\) etc. Alle Punkte zusammen ergeben den Verlauf der Funktion \(f(x)\).
Wenn eine Funktion eine Zuweisung von einem Wert zu einem anderen Wert ist, liegt es auf der Hand, dass man sie als Wertetabelle aufschreiben kann. Die Wertetabelle eignet sich vor allem (aber nicht nur) für Funktionen mit abzählbaren Werten, z.B. wenn der Definitionsbereich aus den natürlichen Zahlen besteht.
Der Funktionsgraph gibt uns einen Überblick, über das Verhalten der Funktion und eine Schätzung für die Werte zwischen den natürlichen \(x\)-Werten. Um den Graphen zu konstruieren, benutzen wir das Argument \(x\) und den Funktionswert \(y=f(x)\), d.h. Punkte im \(x,y\)-Koordinatensystem mit den Koordinaten \(\bigl ( x,f(x) \bigr )\).
Beispiel
Stelle für die Funktion \(f(x)=\frac{1}{10}(x+2)^3\) eine Wertetabelle auf und skizziere anschliessend den Funktionsgraphen.
Die Wertetabelle hat zwei Zeilen: In der ersten Zeile sind die \(x\)-Werte, die wir betrachten möchten. Meistens wählen wir da Werte um den 0-Wert herum, d.h. ein paar negative ganze Zahlen und ein paar positive ganze Zahlen. Wir wählen ganze Zahlen, weil sie einfacher zum Rechnen sind. Wir können aber auch Hälften, Drittel, Viertel etc. einsetzen.
Die zweite Zeile enthält die Funktionswerte, die wir mit den entsprechenden \(x\)-Werten erhalten. Für unsere Funktion kriegen wir z.B. folgende Tabelle:
| \(x\) | -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 |
| \(f(x)\) | -2.7 | -0.8 | -0.1 | 0 | 0.1 | 0.8 | 2.7 | 6.4 |
Bevor wir den Graphen zeichnen, schauen wir kurz den Bereich der Zahlen an:
- Die \(x\)-Werte bewegen sich im Bereich -5 bis 2
- Die \(y\)-Werte decken grob den Bereich -3 bis 7
Jetzt zeichnen wir das Koordinatensystem und setzen das Kreuz mehr oder weniger in die Mitte. In unserem Fall dürften wir das Kreuz auch ein bisschen nach rechts unten legen, weil wir mehr negative \(x\)-Werte und mehr positive \(y\)-Werte haben. Jetzt setzen wir die Skala.
Idealerweise benutzen wir für die \(x\)- und die \(y\)-Achse den gleichen Massstab, weil es sonst zu Verzerrungen kommt. In Ausnahmefällen müssen wir aber die Skala anders wählen, damit wir die Punkte überhaupt zeichnen können.
Jetzt können wir die Punkte aus der Wertetabelle eintragen. Es lohnt sich die Hilfslinien zu den Punkten zu zeichnen. Damit können wir die Koordinaten der Punkte im Nachhinein besser aus dem Diagramm ablesen.
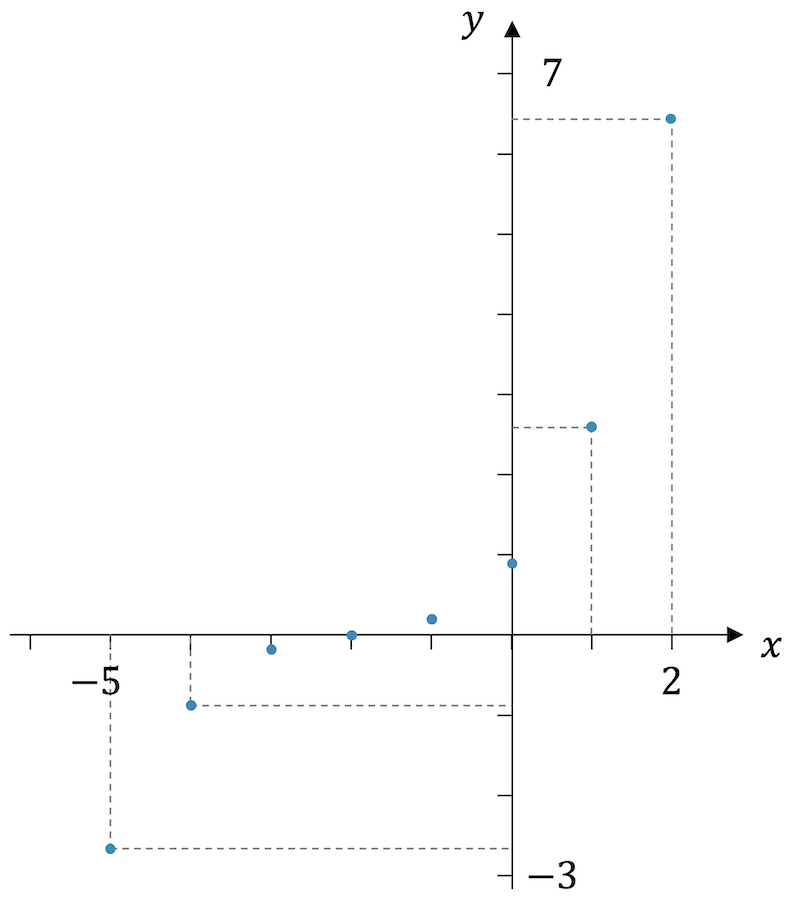
Sobald wir die Punkte haben, erkennen wir den Verlauf des Graphen. Wir verbinden einfach die Punkte so gut es geht. Es geht hier mehr um den Gesamteindruck und weniger um Präzision. Wer es präziser haben will, kann den Verlauf auf dem Computer darstellen und dann beliebig genau reinzoomen.
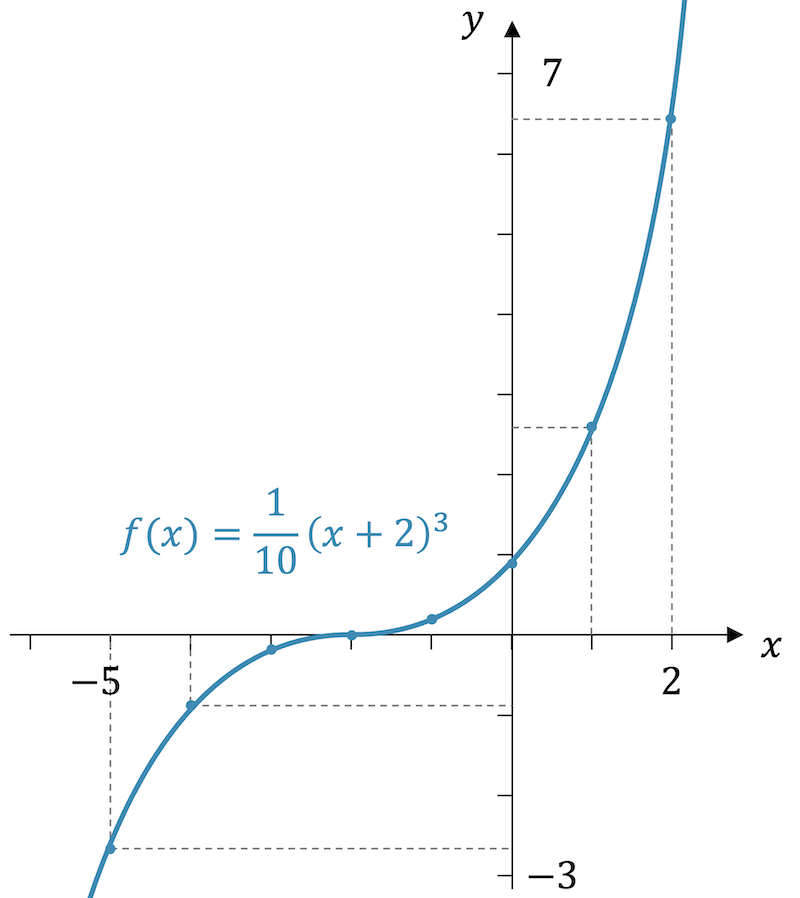
Funktionen von abzählbaren Werten können gut mit einer Wertetabelle beschrieben werden.
Funktionen mit nicht abzählbaren Werten, werden besser mit einem Funktionsgraphen dargestellt: Die Zahlenpaare \(\big( x,y(x) \big)\) bzw. \(\big( x,f(x) \big)\) erzeugen die Punktschar, die als Funktionsgraphen in einem \(x,y\)-Koordinatensystem gezeichnet werden können.
Beispiel
Wie sieht der Funktionsgraph der folgenden Funktionsgleichung aus?
\[ y(x)=\frac{x^2-1}{x} \]
- Wir sehen, dass wir einen Bruch und somit einen Nenner haben. Der Nenner darf nicht null sein, d.h. \(x=0\) ist von der Definitionsmenge \(\boldsymbol{D}\) ausgeschlossen und die Funktion wird an dieser Stelle unstetig sein.
- Wenn der Zähler null ist, ist der ganze Funktionswert null, d.h. wir haben dann eine Nullstelle. Wir können den Zähler in seine Faktoren zerlegen, um die Nullstellen zu bekommen: Der Zähler \(x^2-1\) ist eine binomische Formel (\((a+b)(a-b)=a^2-b^2\)), d.h. \(x^2-1 = (x-1)(x+1)\) und die Nullstellen sind -1 und +1.
- Der Zähler ist eine Potenz zweiten Grades, der Nenner eine Potenz ersten Grades, d.h. der Zähler ist für grosse \(x\)-Werte mächtiger als der Nenner. Wenn wir immer weiter nach rechts gehen (\(x \rightarrow \infty\)) wird der Zähler gewinnen und der Funktionsgraph wird ins Unendliche wachsen, d.h. nach rechts oben. Wir können sogar sagen, dass für sehr grosse \(x\) gilt: \(x^2-1 \approx x^2\) und somit kürzt sich der Bruch zu \(x\). Für grosse \(x\) gleicht der Funktionsgraph immer mehr einer linearen Funktion \(f(x)=x\).
- Die Überlegungen zu den grossen \(x\)-Werten gelten auch für ganz links, wo die \(x\)-Werte vom Betrag her sehr gross sind, aber ein negatives Vorzeichen haben. Für \(x \rightarrow -\infty\) ähnelt der Funktionsgraph auch immer mehr der linearen Funktion \(f(x)=x\), je weiter links wir sind.
- Was passiert in der Mitte, wo die \(x\)-Werte sehr klein sind und wir nahe an der Unstetigkeitsstelle sind? Für \(x\)-Werte, die im Betrag kleiner 1 sind, kippt das Blatt. Das Quadrat macht sie die Zahl sehr klein. Irgendwann ist sie so klein, dass wir sagen können \(x^2-1 \approx -1\). Die Funktionsgleichung verkümmert damit zu \(y(x) \approx \frac{-1}{x}\) und wir haben eine umgekehrte Hyperbel, die bei \(x=0\) ins Unendliche geht.
Zusammengefasst: Wir haben einen Graphen, der von links unten daherkommt, wie die lineare Funktion \(f(x)=x\), bei -1 eine Nullstelle hat, von da an positiv ist, dann aber für \(x=0\) gegen Unendlich geht, wie eine Hyperbel. Auf der rechten Seite, für positive \(x\)-Werte, kommt die Kurve aus dem \(-\infty\), durchbricht die x-Achse bei der Nullstelle +1 und fügt sich dann weiter rechts wieder der linearen Funktion \(f(x)=x\) an.
Wenn du den Funktionsgraphen anschaust, so fällt dir auch noch eine Symmetrie auf, nämlich eine Punktsymmetrie um den Nullpunkt. Tatsächlich ist die Funktion ungerade. Wir können das sehr schnell beweisen, wenn wir die Definition der ungeraden Funktion aufzeigen können, nämlich \(f(-x)=-f(-x)\). Dazu geben wir der Funktion statt \(x\) einfach den Input \((-x)\):
\[ f\Big( (-x) \Big) = \frac{(-x)^2-1}{(-x)} = \frac{x^2-1}{-x} = -\frac{x^2-1}{x} = -f(x) \]
Wenn \(f(-x)=-f(x)\) ist, dann folgt daraus sofort \(-f(-x)=f(x)\) und das entspricht der Definition der ungeraden Funktionen.
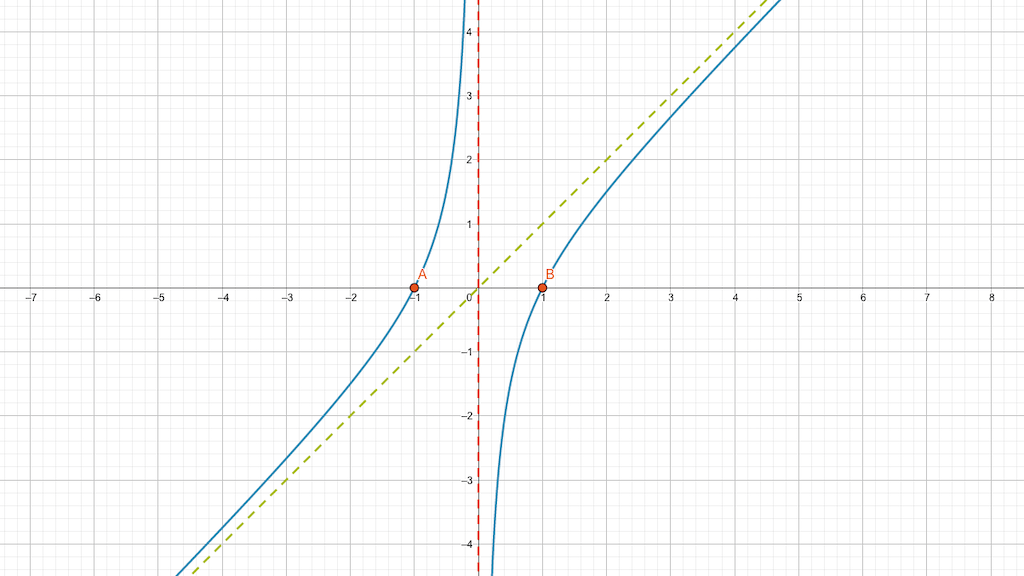
”Kochrezept” für das Skizzieren von Funktionsgraphen:
- Wie verhält sich die Funktionsgleichung für \(x \rightarrow \infty\) (ganz rechts) und für \(x \rightarrow -\infty\) (ganz links). Welche Teile sind mächtiger als andere? Gleicht sich die Funktionsgleichung einer anderen, einfacheren und bekannten Funktionsgleichung an?
- Wie verhält sich die Funktionsgleichung für sehr kleine \(x\)-Werte (\(x \rightarrow 0\))?
- Gibt es Nullstellen?
- Gibt es Definitionslücken bzw. Unstetigkeitsstellen?
- Gibt es Symmetrien? (Ist die Funktion ev. gerade oder ungerade?)
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.
Inhalt






Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.