Inhalt
Das Wichtigste in Kürze
Verschiebung des Funktionsverlaufs in vertikaler Richtung:
Wenn die Original-Funktion \(f(x)\) umd den Betrag \(d\) verschoben wird, entsteht die verschobene neue Funktion \(g(x)\):
\[ g(x)=f(x)+\boldsymbol{d} \]
Dabei ist der Graph von \(g(x)\) um \(d\) nach oben verschoben. Wenn \(d\) negativ ist, entsprechend nach unten.
Verschiebung des Funktionsverlaufs in horizontaler Richtung:
Die Funktion \(f(x)\) um den Betrag \(d\) nach rechts verschoben, ergibt uns die neue Funktion \(h(x)\):
\[ h(x)=f(x-\boldsymbol{d}) \]
Um den Funktionsverlauf nach links zu verschieben, wird der Wert \(d\) addiert:
\[ h(x)=f(x+\boldsymbol{d}) \]
Für das horizontale Verschieben, wird die Funktionsvariabel, d.h. das Argument der Funktion in der Klammer verändert.
Videos
Häufigste Fragen
Verschiebung in vertikaler Richtung
Wir können den Funktionsverlauf im Koordinatensystem sehr einfach nach oben oder unten verschieben. Es reicht den Verschiebungsbetrag zum Funktionswert \(y=f(x)\) zu addieren und schon verschieben sich alle Punkte nach oben.
Deshalb wird für eine Verschiebung nach oben, einfach der Betrag \(d\), um welchen die Funktion nach oben verschoben werden soll, hinzuaddiert, z.B.
\[ f(x)=\sin(x) \quad \rightarrow \quad g(x)=\sin(x)+1 \]
Die Funktion \(f(x)\) schwingt zwischen +1 und -1. Die verschobene Funktion \(g(x)\) hat den gleichen Verlauf, wie \(f\), jedoch um 1 nach oben verschoben. Sie pendelt deshalb zwischen 0 und 2.
\[ g(x)=f(x)+\boldsymbol{d} \]
Dabei entspricht der Graph von \(g(x)\) dem Graphen von \(f(x)\), jedoch um \(d\) nach oben verschoben.
Wenn \(d\) eine negative Zahl ist, entspricht das einer Verschiebung nach unten, z.B. schwingt die Funktion \(h(x)\) (Sinus-Funktion um 2 nach unten verschoben), zwischen den Werten -1 und -3 statt zwischen -1 und +1:
\[ f(x)=\sin(x) \quad \rightarrow \quad h(x)=\sin(x)-2 \]
Die gleiche Philosophie gilt auch beim Strecken und Stauchen der Funktion in \(y\)-Richtung!
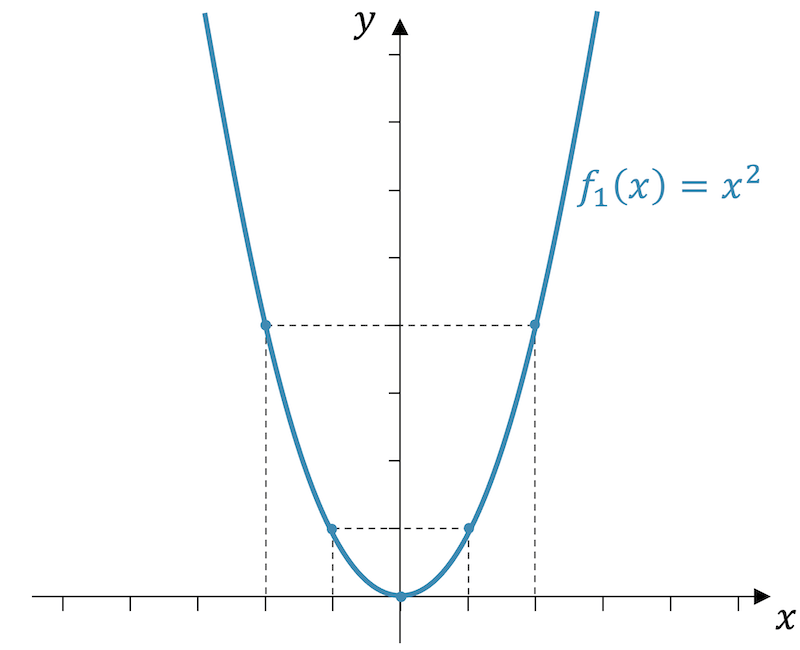
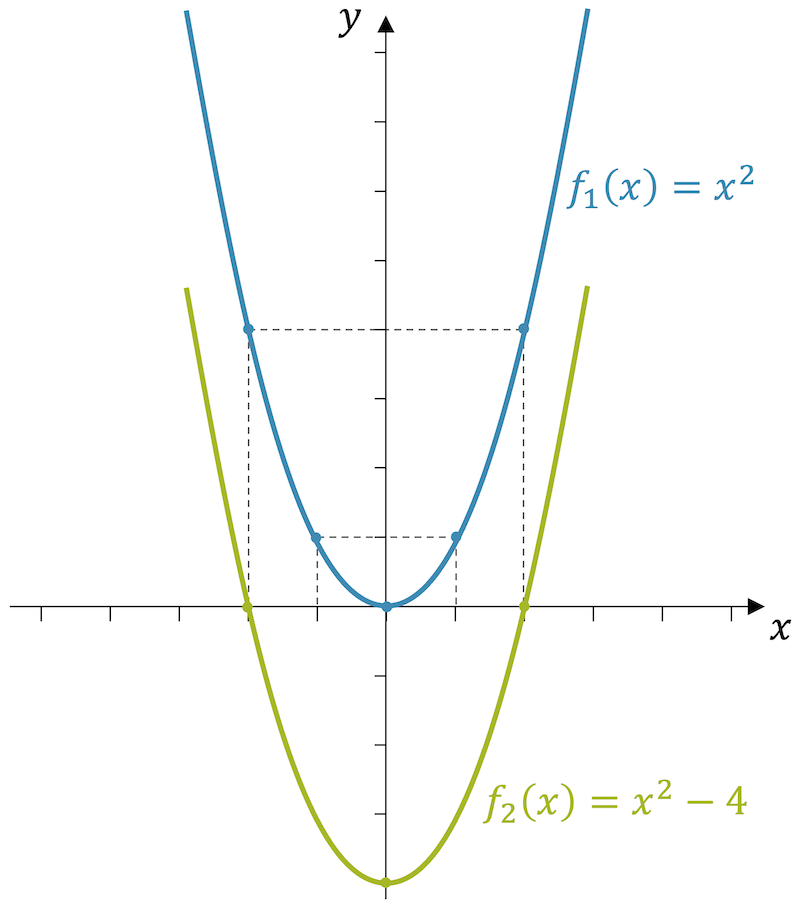
Beispiel: Parabel nach unten verschieben
Verschiebe die Parabelfunktion \(f_1(x)=x^2\) so nach unten, dass der Achsabschnitt (-4) beträgt. Bestimme die neue Funktionsgleichung von \(f_2(x)\) und zeichne den Graphen ein. Erkennst du die beiden neuen Nullstellen in der Funktionsgleichung?
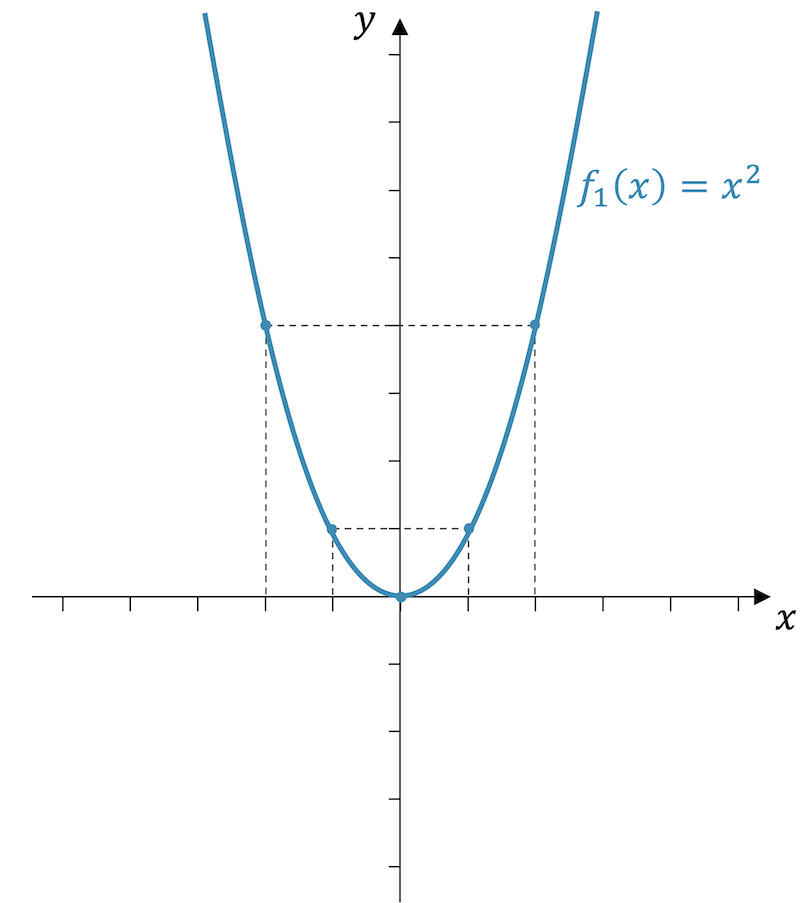
“Die vertikale Verschiebung geschieht am Funktionswert, die horizontale Verschiebung findet an der Funktionsvariablen, statt”
Verschiebung in horizontaler Richtung
Bei der Verschiebung nach oben bzw. unten, haben wir in \(y\)-Richtung verschoben. Wir haben deshalb am Funktionswert geschraubt:
\[ y = f(x) \quad \rightarrow \quad y=g(x)=f(x)+d \]
Wenn der Funktionsverlauf horizontal verschoben wird, müssen wir an der Funktionsvariablen \(x\) schrauben, d.h. am Argument der Funktion. Dafür gehen wir wirklich in die Funktion rein und ersetzen \(x\) mit:
- \((x-d)\) für eine Verschiebung um \(d\) nach rechts
- mit \((x+d)\) für eine Verschiebung nach links
\[ y = f(x) \quad \rightarrow \quad y=g(x)=f(x \pm d) \]
Beachte, dass wir nicht das \(y\) um \(d\) grösser/kleiner machen, sondern in der Funktionsklammer drin das \(x\) vergrössern bzw. verkleinern.
Verschiebung des Funktionsverlaufs in horizontaler Richtung:
Wir können auch einen neuen Funktionsgraphen \(g(x)\) erhalten, der um den Betrag \(\boldsymbol{d}\) nach rechts verschoben ist, mit:
\[ y = f(x) \quad \rightarrow \quad y=g(x)=f(x – d) \]
Wenn \(\boldsymbol{d}\) negativ ist, d.h. in der Klammer ein Wert zum Argument hinzuaddiert wird, verschiebt sich der Verlauf entsprechend nach links:
\[ y = f(x) \quad \rightarrow \quad y=g(x)=f(x + d) \]
Beispiel: Parabel nach links verschieben
Verschiebe die Parabelfunktion \(f_1(x)=x^2\) so nach links, dass der Achsabschnitt (+4) beträgt. Bestimme die neue Funktionsgleichung von \(f_3(x)\) und zeichne den Graphen ein. Erkennst du die neue Nullstelle in der Funktionsgleichung?
Aufgabensammlung
Lernziele
- Du kannst gegebene Funktionen vertikal und horizontal verschieben und die neuen Funktionsgleichungen hinschreiben
- Du kannst (in einfachen Fällen) den Vorgang des Verschiebens rückgängig machen und so eine Funktion als Verschiebung einer anderen Funktion deuten.
Weitere Links
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.
Inhalt


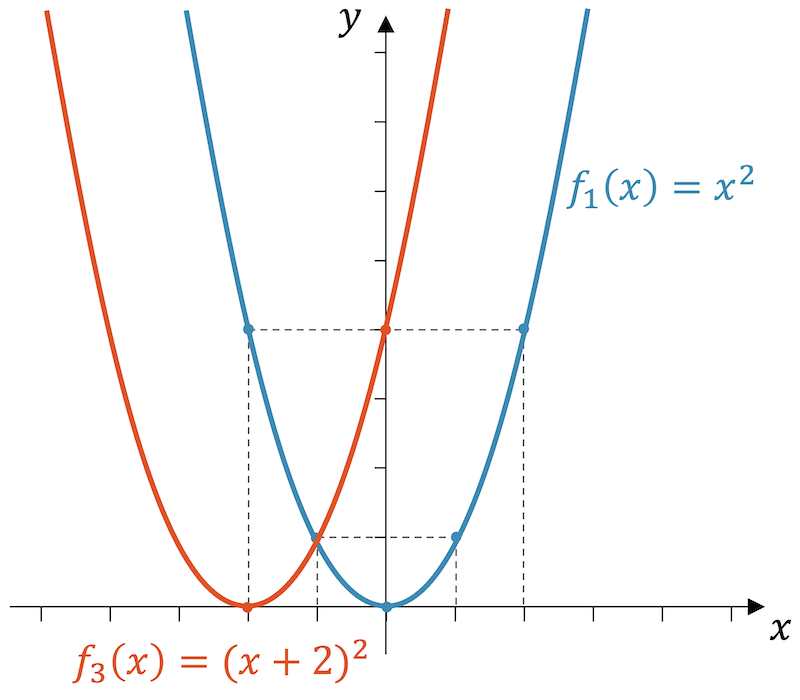





Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.