Inhalt
Die harmonische Folge ist definiert als \(a_n = \frac{1}{n}\). Mit immer grösser werdendem Zähler werden die Glieder der Folge immer kleiner, wie wir es im Plot sehr schön sehen können.
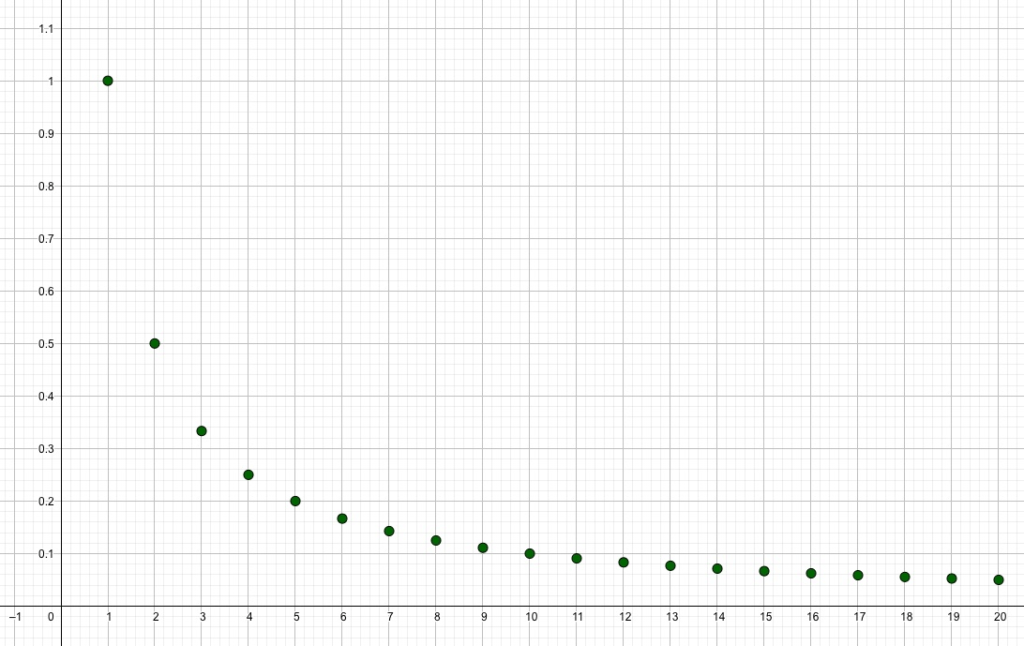
Die zu dieser Folge gehörende harmonische Reihe hat eine erstaunliche Eigenschaft. Die Glieder der Reihe werden immer grösser ohne dass sie sich einem Wert annähern. Sie steigen und steigen und im Unendlichen werden sie unendlich gross! Man sagt auch, dass die Reihe divergent ist, d.h. im Unendlichen “quasi explodiert”.
Beachten Sie, dass die Folgen \(b_n = \frac{1}{n^2}\) oder \(c_n = \frac{1}{n^3}\) etc. Reihen bilden, die sich sehr wohl einem endlichen Wert annähern. Man nennt sie konvergent.
Die harmonische Reihe \(\boldsymbol{s_n}\) ist die Reihe zur konvergenten Folge \(a_n=\frac{1}{n}\). Die harmonische Reihe ist divergent.
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.
Inhalt






Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.