Inhalt
Das Wichtigste in Kürze
Die Punktprobe testet, ob ein Punkt \(Q\) auf einer Geraden \(g\) liegt, d.h. ob es eine Lösung für den Parameter \(\lambda\) gibt, der mit der entsprechenden Gleichung zu diesem Punkt \(Q\) führt:
\[ g:\quad \overrightarrow{OA} \; + \; \lambda \cdot \vec{a} \; = \; \overrightarrow{OQ} \]
Diese Vektorgleichung ist ein Gleichungssystem von 3 Gleichungen und 1 Unbekannte \(\lambda\), d.h. sie ist überbestimmt. Nur eine Gleichung würde für eine Unbekannte reichen, d.h. jetzt gibt es zwei Fälle:
- Die anderen Gleichungen haben die gleiche Lösung für \(\lambda\): \(\;\;Q \in g\)
- Die anderen Gleichungen haben nicht die gleiche Lösung für \(\lambda\): \(\;\;Q \notin g\)
Für die Punktprobe mit einer Ebene \(E\) gilt analog:
\[ E:\quad \overrightarrow{OA} \; + \; \lambda_1 \cdot \vec{a_1} \; + \; \lambda_2 \cdot \vec{a_2} \; = \; \overrightarrow{OQ} \]
Dies entspricht einem Gleichungssystem von 3 Gleichungen mit 2 Unbekannten (\(\lambda_1\) und \(\lambda_2\)), d.h. auch dieses Gleichungssystem ist überbestimmt.
Mit zwei der drei Gleichungen erhalten wir eine Lösung (\(\lambda_1\), \(\lambda_2\)). Die dritte Gleichung ist mit dieser Lösung ebenfalls erfüllt (\(Q \in E\)) oder nicht (\(Q \notin E\)).
Tutorial Videos
Punkt auf der Geraden
Liegt ein Punkt auf einer Geraden oder nicht? Nun, das können wir relativ einfach beantworten. Eine Geradengleichung hat ja die folgende Struktur: Ein Punkt \(A\) auf der Geraden (Stützvektor \(\vec{OA}\)) plus ein Vielfaches (\(\lambda\)) eines Vektors (\(\overrightarrow{AB}\)), der die Richtung der Geraden vorgibt, ergibt einen weiteren Punkt \(P\) auf dieser Geraden. Je nach Faktor \(\lambda\) erhalten wir einen anderen Punkt \(P\). Das gibt schliesslich alle Punkte auf der Geraden:
\[ \overrightarrow{OP} \;\; = \;\; \overrightarrow{OA} + \lambda \cdot \overrightarrow{AB} \]
Wir möchten jetzt wissen, ob ein ganz bestimmter Punkt \(Q\) auf der Geraden liegt, d.h. ob es einen bestimmten Wert für \(\lambda\) gibt, der die Gleichung erfüllt:
\[ \overrightarrow{OQ} \;\;\stackrel{?}{=}\;\; \overrightarrow{OA} + \lambda \cdot \overrightarrow{AB} \]
Das eine Vektorgleichung, d.h. für die einzelnen x-, y- und z-Koordinaten sind es eigentlich drei Gleichungen, die zusammen ein Gleichungssystem bilden:
\[ \begin{cases} \begin{array}{cc} OQ_x \stackrel{?}{=} OA_x + \lambda \cdot AB_x \\ {OQ}_y \stackrel{?}{=} OA_y + \lambda \cdot AB_y \\ OQ_z \stackrel{?}{=} OA_z + \lambda \cdot AB_z \end{array} \end{cases} \]
Jetzt sind das alles Zahlen, nämlich die Komponenten der Vektoren, bis auf \(\lambda\), die Unbekannte. Wir haben ein lineares Gleichungssystem mit drei Gleichungen, aber nur eine Unbekannte!
Ein solches Gleichungssystem wird überbestimmt genannt, denn wir haben zu viele Gleichungen. Für eine Unbekannte reicht eine Gleichung und wir können sie bestimmen.
Was passiert jetzt, wenn wir drei Gleichungen haben? Dazu gibt es zwei Szenarien:
- Die drei Gleichungen sind sich einig und ergeben die gleiche Lösung für \(\lambda\), d.h. dieser Wert erfüllt die Geradengleichung und führt genau zum Punkt \(Q\), der somit auf der Geraden liegt.
- Die drei Gleichungen sind sich uneinig über den Lösungswert von \(\lambda\), d.h. wir können den Punkt \(Q\) nicht mit der Geradengleichung erreichen, weil er schon gar nicht auf \(Q\) liegt.
Wir werden deshalb versuchen das Gleichungssystem zu lösen. Falls wir in allen drei Gleichungen die gleiche Lösung für \(\lambda\) erhalten, gilt \(Q \in g\), falls aber irgendein Widerspruch auftaucht, dann gilt \(Q \notin g\).
Beispiel
Punkt auf der Ebene
Für die Punktprobe mit einer Ebene gehen wir genau gleich vor. Mit der folgenden Ebenengleichung erreichen wir alle Punkte \(P\) auf der Ebene \(E\). Dazu haben wir zwei Stellschrauben, die beiden Parameter \(\lambda_1\) und \(\lambda_2\), die sämtliche Werte annehmen können:
\[ \overrightarrow{OP} \;\; = \;\; \overrightarrow{OA} \; + \; \lambda_1 \cdot \vec{a_1} \; + \; \lambda_2 \cdot \vec{a_2}\]
Jetzt möchten wir aber wissen, ob ein ganz bestimmter Punkt \(Q(Q_x,Q_y,Q_z)\) auf der Ebene \(E\) ist, oder nicht. Wir nehmen seinen Ortsvektor und setzen ihn mit der Ebenengleichung gleich.
\[ \overrightarrow{OQ} \;\; = \;\; \overrightarrow{OA} \; + \; \lambda_1 \cdot \vec{a_1} \; + \; \lambda_2 \cdot \vec{a_2}\]
Diese Vektorgleichung entspricht einem Gleichungssystem von 3 Gleichungen mit 2 Unbekannten \(\lambda_1\) und \(\lambda_2\).
\[ \begin{cases} \begin{array}{cc} OQ_x – OA_x = a_{1,x} \;\lambda_1 + a_{2,x} \;\lambda_2 \\ OQ_y – OA_y = a_{1,y} \;\lambda_1 + a_{2,y} \;\lambda_2 \\ OQ_z – OA_z = a_{1,z} \;\lambda_1 + a_{2,z} \;\lambda_2 \end{array} \end{cases} \]
Das Gleichungssysstem ist überbestimmt, d.h. zwei Gleichungen reichen für die Bestimmung der Lösung (\(\lambda_1\), \(\lambda_2\)). Die dritte Gleichung ist entweder mit dem Resultat der beiden anderen Gleichungen einverstanden oder nicht:
- Erfüllen (\(\lambda_1\), \(\lambda_2\)) die dritte Gleichung, so gilt: \(Q \in E\)
- Ist die dritte Gleichung durch (\(\lambda_1\), \(\lambda_2\)) nicht erfüllt, gilt \(Q \notin E\).
Beispiel
Weitere Videos
(keine externe Youtube-Videos zu diesem Thema)
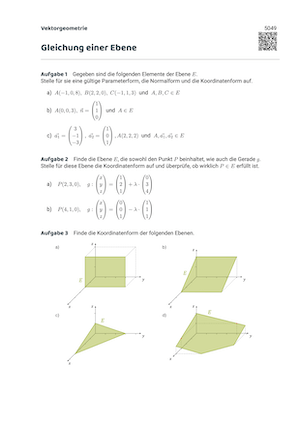
Aufgabensammlung
Mini-Test
Um Zugang zum Mini-Test zu kriegen,
musst du vollwertiges Mitglied im Hacker-Club sein.
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.
Inhalt











Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.