Platonische Körper

Der griechische Philosoph Platon (428/427 – 348/347 v. Chr.) war ein Schüler von Sokrates und Lehrer von Aristoteles. In einem seiner philosophischen Werke beschreibt Platon, wie ein Schöpfer die dingliche Welt aus der Ur-Materie gestaltet haben soll. Die vier Elemente (Feuer, Luft, Wasser und Erde) und der Äther als fünftes Element sind die perfekten Grundformen der vom Schöpfer gestalteten Materie, die die Natur ausmachen. Die Perfektion ist mathematischer Natur in dem es die einzigen dreidimensionalen Körper sind, die aus regelmässigen Polyederflächen zusammengesetzt werden können. Mit diesen Grundbausteinen der Materie, einer Art “geometrischer Atome”, begründete Platon eine Vorstellung einer Art atomaren Struktur der Materie.

Alle platonischen Körper haben die folgenden Eigenschaften:

• Alle Seitenflächen sind gleich
• Sie sind konvex, d.h. sie haben ausschliesslich nach aussen gerichtete Ecken und Kanten
• Zu den Ecken führen immer die gleiche Anzahl Kanten zusammen
• Die Kantenlänge ist immer gleich
• Alle Ecken, Kanten und Seitenflächen können durch Rotationen ineinander überführt werden
• Alle Ecken haben den gleichen Abstand zum Mittelpunkt, d.h. der platonische Körper passt genau in eine Umkugel hinein
• Alle Mittelpunkte der Seitenflächen haben den gleichen Abstand zum Mittelpunkt, d.h. im platonischen Körper passt genau eine Inkugel hinein

Tetraeder

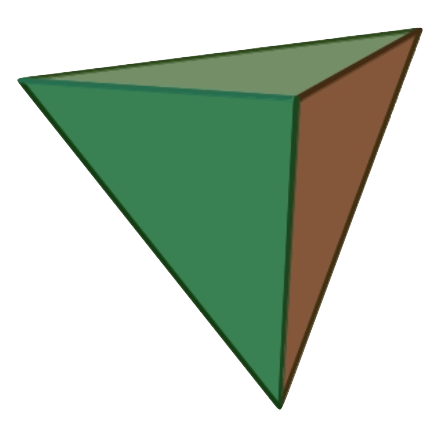
4 Dreiecke, 6 Kanten, 4 Ecken

Hexaeder (Würfel)

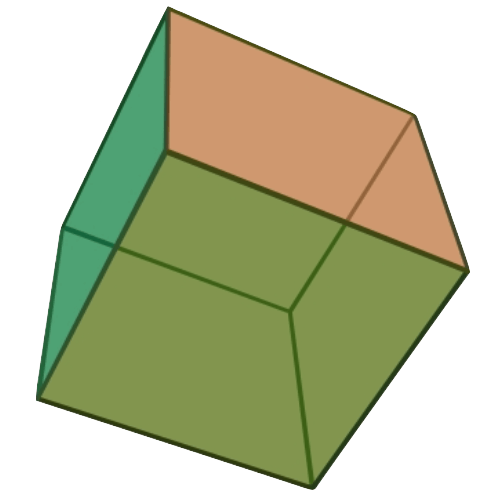
6 Quadrate, 12 Kanten, 8 Ecken

Oktaeder

8 Dreiecke, 12 Kanten, 6 Ecken

Dodekaeder

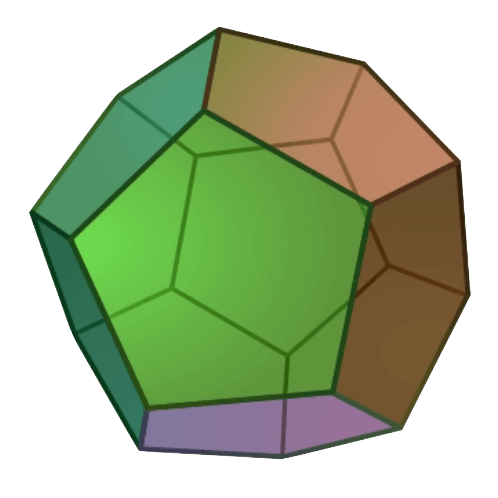
12 Fünfecke, 30 Kanten, 20 Ecken

Ikosaeder

20 Dreiecke, 30 Kanten, 12 Ecken

Mittlerweile kennen unsere Naturwissenschaften den Aufbau der Materie sehr gut. Stellt sich also die Frage: Hatte Platon recht?. Nicht wirklich. Die platonischen Körper sind aus mathematischer Sicht wunderbare, symmetrische Objekte. In der Natur finden wir zwar gewisse Spuren, aber damit hat es sich leider auch schon.

Das berühmteste Tetraeder kennst du vielleicht aus der Chemie. Das Kohlenstoffatom bildet sog. \(sp^3\)-Hybridorbitale, die eine vierfache Elektronenbindung erlaubt. Die vier Bindungen liegen räumlich in den Ecken eines Tetraeders. Auf diese Art können wir uns Moleküle wie das Methan \(CH_4\) räumlich vorstellen. Viele Kristalle, darunter sehr viele Metalle, sind aufgrund der Tetraederstruktur aufgebaut, denn sie bietet die dichteste Packung.

Das Hexaeder, besser bekannt als Würfel gibt es ebenfalls in der Natur. Gewisse Kristalle (z.B. Polonium) bilden die sog. simple cubic-Struktur. Allerdings ist diese Struktur im Vergleich zu anderen Strukturen nicht sehr günstig, da sie nicht optimal dicht gepackt ist, d.h. es entstehen grössere Lücken als im Fall einer tetraedischen Kombination. Deshalb treffen wir diese Kristallform viel seltener an, als die anderen, dichter gepackten Strukturen.

In der Chemie finden wir das Oktaeder in gewissen oktaedrischen Molekülen. Auch gibt es Kristallstrukturen, wie das Natriumchlorid (Kochsalz), das aus vielen oktaedrischen Elementarzellen besteht.

Gewisse Kristalle des Pyrits bilden schöne makroskopische Dodekaeder, allerdings muss man hier anmerken, dass die darunterliegende Kristallstruktur keine Dodekaederstruktur ist. Das Dodekaeder scheint in der Natur nicht wirklich vorzukommen. Das kleinste der Fullerene ist ein Dodekaeder. Fullerene sind regelmässige und geschlossene (“kugelförmige”) Moleküle mit fünf- und sechseckigen Kohlenstoffringen.

Schliesslich haben wir das Ikosaeder: Wir finden es bei vielen bekannten Viren, die ihr Genom in einer ikosaedrischen Proteinkapsel (Kapsid) verpackt haben, so z.B. das Rhinovirus (Schnupfen), Hepatitis-B-Virus, Poliovirus etc.

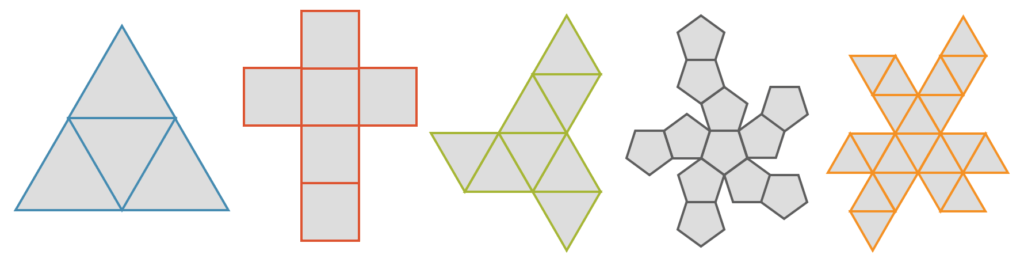
Körpernetze

Da die platonischen Körper flache Seiten haben, können wir sie auch zweidimensional mit ihren Körpernetzen beschreiben, d.h. Figuren, die alle Seitenflächen und Kanten beinhalten. Die Raumwinkel wurden aber alle zu \(180°\) flachgedrückt. Mit Hilfe eines Körpernetzes kann ein platonischer Körper aus einem Blatt Papier ausgeschnitten und anschliessend geformt werden. Die Anordnung der Seitenflächen ist nicht ganz beliebig, aber es gibt viele gültige Varianten.

Der Euler’sche Polyedersatz

Der Euler’sche Polyedersatz gilt nicht nur für platonische Körper, sondern ganz allgemein für beschränkte und konvexe Polyeder. Er besagt, dass die Anzahl Ecken \(E\) minus die Anzahl Kanten \(K\) plus die Anzahl Flächen \(F\) für solche Körper immer gleich zwei sind:

\[ E – K + F = 2\]

Name	Ecken \(E\)	Kanten \(K\)	Flächen \(F\)	\)E-K+F\)
Tetraeder	4	6	4	2
Hexaeder	8	12	6	2
Oktaeder	6	12	8	2
Dodekaeder	20	30	12	2
Ikosaeder	12	30	20	2

Nur fünf platonische Körper

Um zu verstehen, dass es nicht mehr als fünf platonische Körper gibt oder geben kann, schauen wir uns deren Ecken genauer an. Den fünf platonischen Körpern ist gemeinsam, dass sie konvexe Ecken haben, d.h. Ecken, die aus dem Körper herausragen. Was macht eine konvexe Ecke aus? Wir schauen uns das zuerst an einem nicht-konvexen Beispiel an: Wenn wir z.B. ein drei Ländereck auf der Landkarte nehmen, dann stossen drei Flächen in einem Punkt zusammen. Die Summe der drei Winkel muss auf jeden Fall 360° ergeben.

Jetzt vergleichen wir das mit dem Würfel: An seinen Ecken treffen drei Quadratflächen zusammen. Jedes Quadrat hat einen Flächenwinkel von 90°. Diese drei Winkel summieren sich bloss zu \(3 \cdot 90° = 270°\). Sobald die Summe der Winkel kleiner ist als 360° haben wir eine konvexe Ecke. Wir könnten sogar sagen, dass die Ecke umso spitzer ist, je kleiner die Summe der Flächenwinkel beträgt.

Eine andere Argumentation wäre: Um eine Würfelecke zu basteln, brauchen wir drei Quadrate, die über zwei Kanten zusammenhängen. Ein solches Netz ist noch flach wie das Papier. Sobald wir es aber an der dritten Kante zusammenbringen, entsteht die Räumlichkeit und damit die konvexe Würfelecke. Mit dem Zusammenbringen der “beiden” dritten Kanten zu einer, zwingen wir die drei Winkel von je \(90°\), den “Kreis” um die Ecke trotzdem zu schliessen.

Um einen Körper zu bilden braucht es mindestens drei Flächen. Zwei Flächen ergeben zusammen nur ein flache “Scheibe” und noch keinen Körper. Genauso braucht es mindestens drei Ecken, damit eine Seite auch eine Fläche ist. Ein “Zweieck” wäre nur eine Strecke und noch keine Fläche.

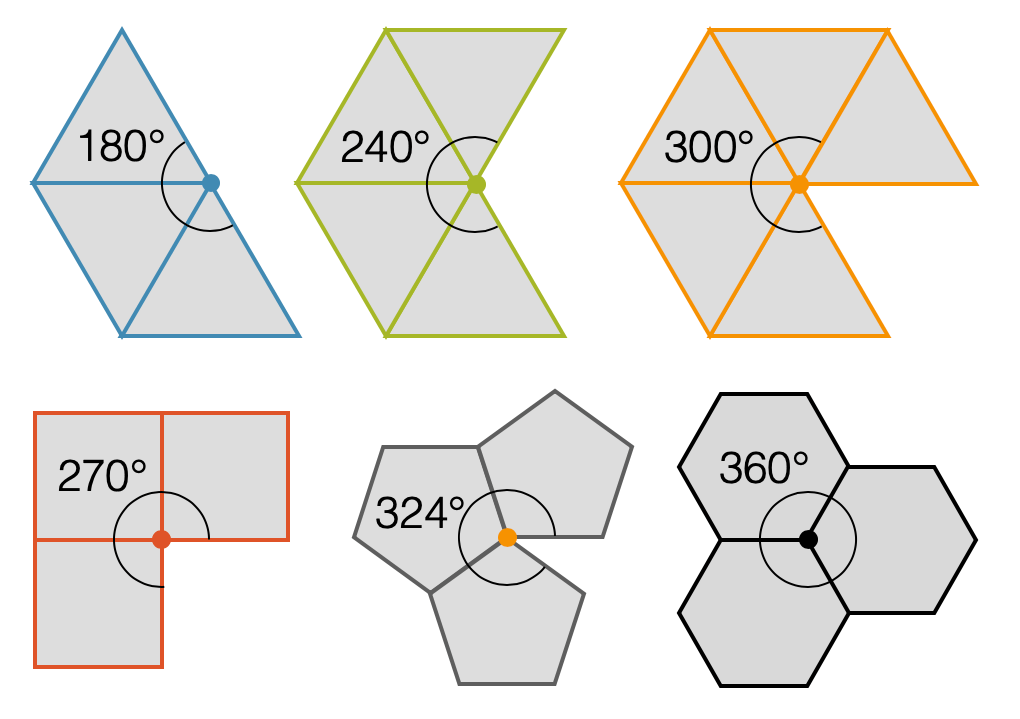
Wir starten deshalb mit dreieckigen Seitenflächen (regelmässige Dreiecke) und versuchen eine konvexe Körperecke zu bauen. Mit drei solchen Dreiecken beträgt die Summe der Winkel 180° und somit haben wir eine relativ spitze Körperecke. Es ist die Körperecke des Tetraeders, unserem ersten platonischen Körper.

Kombinieren wir vier solche Dreiecke, ergibt es eine Summe von 240° und der Körper ist ein Oktaeder. Auch fünf Dreiecke passen noch: Sie ergeben eine Summe von 300° und wir erschaffen damit das Ikosaeder. Jetzt ist klar, dass 63 hätte eine Summe von 360° ergeben und das gibt uns keine konvexe Ecke mehr. Sie ist flach, d.h. wir haben damit die Möglichkeiten mit regelmässigen Dreiecken einen platonischen Körper zu bauen ausgeschöpft.

Wir greifen deshalb zum regelmässigen Viereck (Quadrat) und starten wieder bei der Mindestzahl von drei Seitenflächen. Es klappt! Die Summe beträgt 270° und wir haben den Hexaeder (Würfel). Vier Quadrate würden in Summe wieder 360° ergeben d.h. wir können keinen weiteren Körper mit Quadraten bilden.

Schalten wir deshalb noch einmal hoch zum regelmässigen Fünfeck: Zuerst müssen wir bestimmen, wie gross der Flächenwinkel im Fünfeck ist. Wäre das Fünfeck ein Kuchen, so könnten wir fünf gleich Dreieck schneiden. Der Scheitelwinkel wäre dann \(360° : 5 = 72°\). Da es sich um gleichschenklige Dreiecke handelt, wären die beiden anderen Winkel je \((180° – 72°): 2 = 54°\). Der Winkel in einer Ecke eines Fünfecks wird durch zwei solche Winkel gebildet, d.h. er beträgt \(2 \cdot 54° = 180°\). Damit summieren sich die Flächenwinkel der drei Fünfecke zu 324°. Das passt und wir haben den Dodekaeder gefunden. Vier Fünfecke gehen nicht mehr, da die Summe grösser ist als 360°.

Wir verlassen die Fünfecke und gehen über zu den Sechsecken. Die Summe von drei Winkeln beträgt jetzt 360° und wir können damit keine konvexe Körperecke mehr bilden, höchstens eine flache Bienenwabe. Mit Siebenecken beträgt der Winkel von drei Flächen bereits \(3 \cdot 128.57° = 385.71°\), d.h. wir können keine konvexe Ecke mehr bilden. Es gibt deshalb nur fünf platonische Körper!

Euklid von Alexandria, ein bedeutender griechischer Mathematiker, der vermutlich im 3. Jahrhundert v. Chr. lebte, soll auf diese Weise als Erster bewiesen haben, dass es nur fünf platonische Körper geben kann.

Name	Anzahl Flächen pro Ecke	Flächenwinkel	Summe aller Flächenwinkel
Tetraeder	3	60°	180°
Hexaeder	3	90°	270°
Oktaeder	4	60°	240°
Dodekaeder	3	108°	324°
Ikosaeder	5	60°	300°