Stetigkeit

Beispiel

Finde die Unstetigkeitsstellen der folgenden Funktion. Um welche Art von Unstetigkeitsstellen handelt es sich?

\[ f(x) = \frac{x^2-1}{x^2-2x-24} \]

---

Wir erhalten die Unstetigkeitsstelle, indem wir das Nennerpolynom null stellen:

\[ x^2-2x-24 \; \overset{!}{=} \; 0 \]

Links können mit mit dem Klammeransatz faktorisieren, denn der zweite Term ist \(4-6=-2\) und der dritte Term ist \(4 \cdot (-6) = -24\). Somit schreiben wir:

\[ (x+4)(x-6) = 0 \]

Wir sehen sofort, dass diese Gleichung erfüllt ist, wenn \(\underline{x=-4}\) oder \(\underline{x=6}\). Das sind unsere beiden Unstetigkeitsstellen.

Um die Art der Unstetigkeitsstellen herauszufinden, machen wir eine kleine Skizze des Graphen. Dazu ermitteln wir noch ein paar Punkte:

\[ f(0) = \frac{1}{24} \]

Das Zählerpolynom verrät uns die Nullstellen der Funktion:

\[ x^2 – 1 \; \overset{!}{=} \; 0 \]

\[ x^2 = 1 \]

Diese Gleichung hat zwei Lösungen: \(x=-1\) und \(x=1\).

Die Polynomdivision verrät uns zudem das Verhalten der Funktion im Unendlichen (Asymptote):

\[ (x^2-1) \;:\; (x^2-2x-24) \; = \; 1 + \text{Rest} \]

Damit schmiegt sich die Funktion der Asymptoten \(y=1\) an für \(x \rightarrow -\infty\) und \(x \rightarrow \infty\).

Der Verlauf der Funktion sieht in etwa folgendermassen aus:

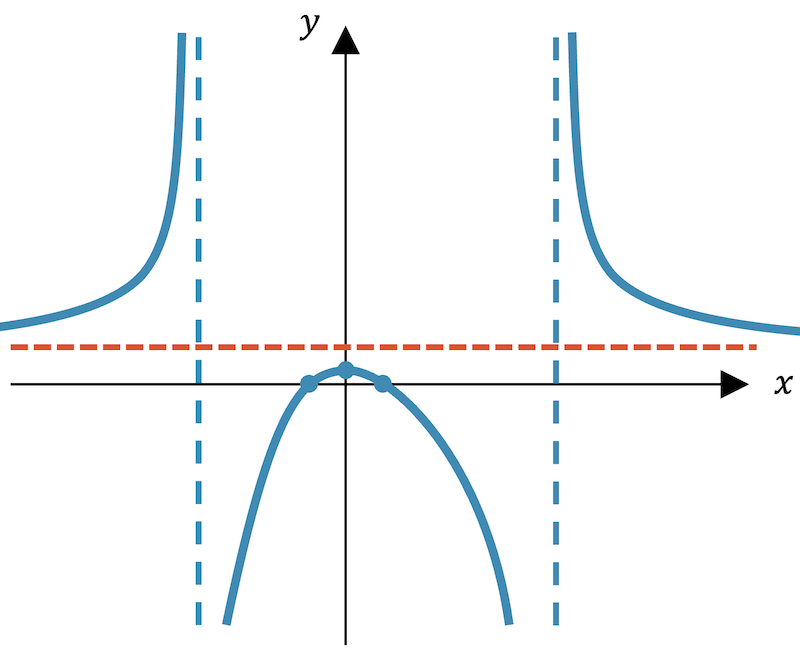
Die beiden Unstetigkeitsstellen sind unendliche Sprünge.

Beispiel

Untersuche die Stetigkeit der folgenden Funktion

\[ y(x)=\frac{x+1}{x-1} \]

---

Die Unstetigkeitsstelle finden wir, indem wir den Nenner auf null setzen. Der Nenner ist null für \(\underline{x=1}\).

Die Funktion hat eine Nullstelle in \(x=-1\), wie wir es im Zählerpolynom sofort erkennen können.

Den Achsabschnitt erhalten wir ebenfalls sehr schnell:

\[ f(0) = \frac{0+1}{0-1} = -1 \]

Schliesslich führen wir eine Polynomdivision durch und erhalten:

\[ (x+1) \;:\; (x-1) \;=\; 1 + \text{Rest} \]

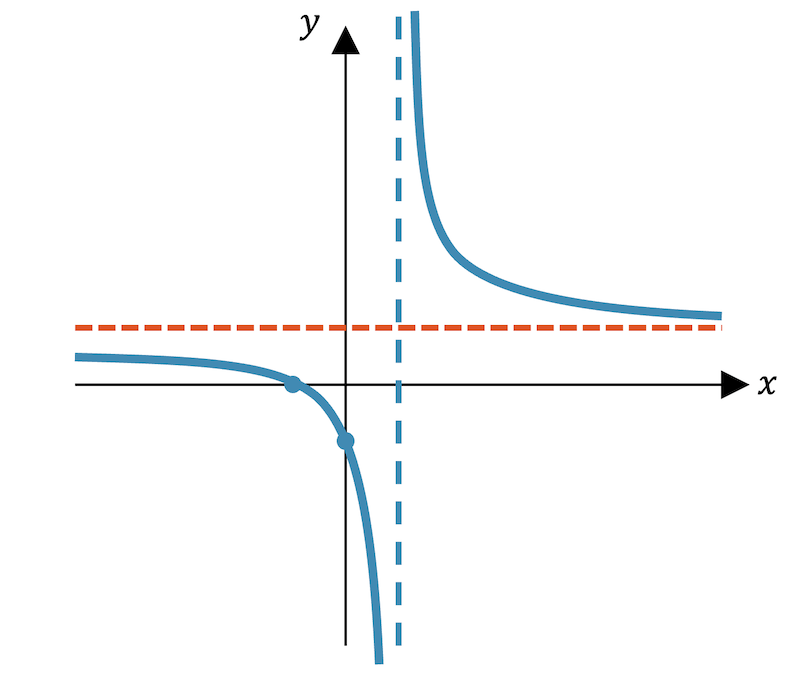
Damit ist die Asymptote wieder von der Form \(y=1\).

Der Verlauf zeigt uns, dass es sich um einen unendlichen Sprung handelt.