ONLINE-KURS

Vektorgeometrie: Meistere die Kunst der räumlichen Berechnungen

Dieser Kurs vermittelt dir die grundlegenden Kenntnisse, um mit Vektoren umzugehen und komplexe Probleme in der Mathematik zu lösen.

In diesem Kurs lernst du, wie du Vektoren in der Geometrie verwenden kannst, um räumliche Geraden und Ebenen zu beschreiben und Abstände, Schnittpunkte und Schnittgeraden zu berechnen.

Du wirst auch das Skalarprodukt, das Vektorprodukt und das Spatprodukt kennenlernen und deren Anwendungen verstehen.

Am Ende des Kurses wirst Du zudem in der Lage sein, Kreise und Kugeln zu beschreiben und mit diesen Definitionen zu rechnen.

Erweitere deine mathematischen Fähigkeiten!

Dieser Kurs umfasst:

  • 74 Videos
  • pdf-Script (105 Seiten)
  • 127 Beispiele, Mini-Übungen und Übungsaufgaben (alle mit vollständiger Lösung)
  • 24 Mini-Tests
  • Abschlusstest mit Zertifikat
  • Totaler Zeitbedarf: ca. 30-50 Stunden

CHF 99

Jetzt kaufen

Nicht der richtige Kurs? Geld-Zurück-Garantie!

Der ganze Stoff und die Übungen und Beispiele werden in Videos erklärt.

Das wirst du lernen:

  • Du kannst mit Vektoren umgehen und kannst mit Vektoren rechnen (Addition, Subtraktion, Multiplikation mit einem Skalar)
  • Du weisst, was kollineare, komplanare Vektoren sind und was wir unter einer Linearkombination von Vektoren verstehen
  • Du kennst das Skalarprodukt, kannst es anwenden und weisst, wofür es genutzt werden kann
  • Du kennst das dreidimensionale Koordinatensystem und weisst, dass Geraden und Ebenen als Mengen von vielen Punkten angesehen werden können, die z.T. gemeinsame Schnittmengen haben können.
  • Du kannst mit demVektorprodukt und dem Spatprodukt rechnen und kennst auch deren Anwendungen
  • Du kannst räumliche Geraden auf verschiedene Arten beschreiben und mit ihnen Abstände, Schnittpunkte etc. rechnen
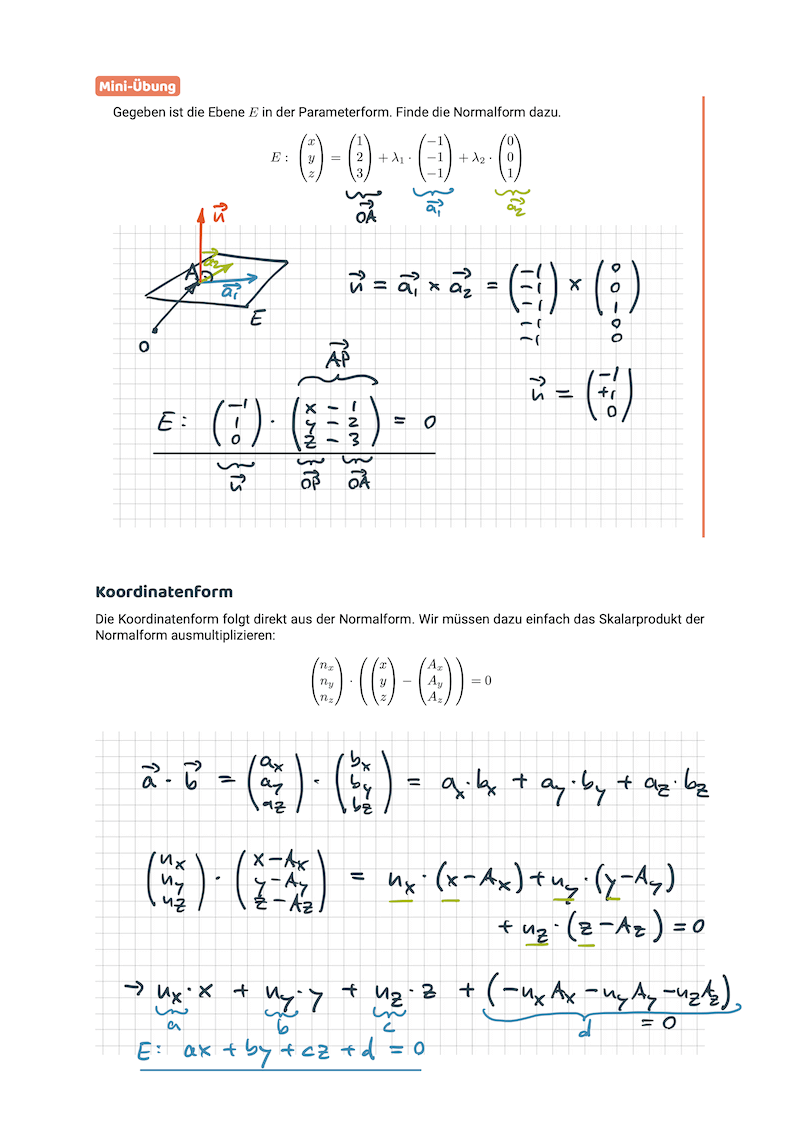
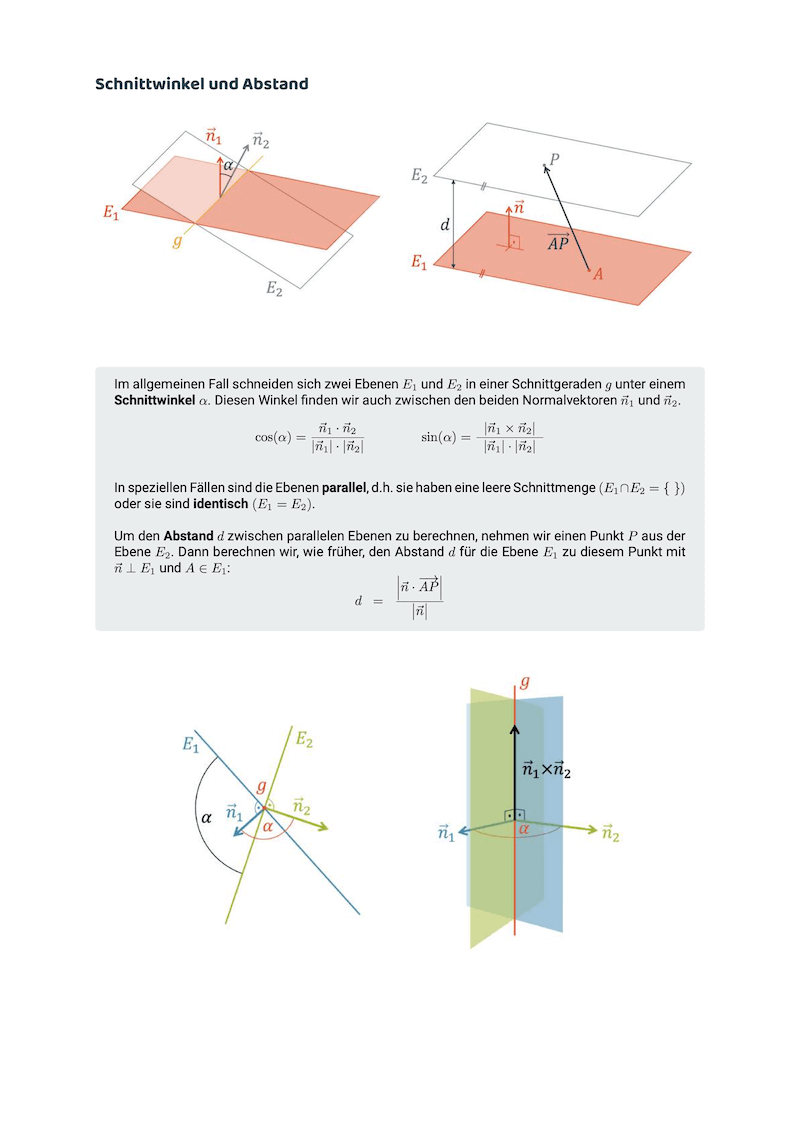
  • Du verstehst, wie Ebenen im Raum beschrieben werden und kannst Schnittpunkte, Schnittgeraden etc. berechnen
  • Du weisst, wie ein Kreis oder eine Kugel beschrieben werden und wie mit diesen Definitionen gerechnet wird

Mit Mini-Tests kannst du deinen Lernfortschritt überprüfen. Zum Schluss gibt es einen Abschluss-Test über alle Inhalte. Wer ihn besteht, kriegt von uns natürlich ein Zertifikat!

Bewertungen: (Sterne), letzmals aktualisiert am 01.01.24

Kursinhalte

    • Kursvideo
    • Kursüberblick und Organisatorisches
    • Herunterladen des Scripts

    • 7 Kursvideos
    • Vektoren als Abbildung von Punkten
    • Vektor aufgrund von zwei Punkten
    • Norm eines Vektors
    • Einheitsvektor
    • Gegenvektor
    • Ortsvektor
    • Mini-Test zu Vektoren

    • 16 Kursvideos
    • Vektoren addieren
    • Vektoren subtrahieren
    • Vektoren zerlegen
    • Vektor mit einem Skalar multiplizieren
    • Kollineare Vektoren
    • Komplanare Vektoren
    • Linearkombination
    • Skalarprodukt
    • 6 Mini-Tests zu Rechnen mit Vektoren

    • 6 Kursvideos
    • Punkte als Elemente
    • Geraden und Ebenen als Mengen
    • Schnittmengen
    • Dreidimensionales Koordinatensystem
    • 2 Mini-Tests zu räumlicher Vektorgeometrie

    • 8 Kursvideos
    • Vektorprodukt in der Komponentenschreibweise
    • Algebraische Eigenschaften
    • Lot auf der Ebene
    • Fläche des Parallelogramms
    • Rechtssystem
    • Spatprodukt
    • 3 Mini-Tests zu Vektor- und Spatprodukt

    • 12 Kursvideos
    • Parameterform
    • Normalform
    • Punkt auf der Geraden
    • Abstand zwischen Punkt und Gerade
    • Gerade und Gerade
    • Zwei sich kreuzende Geraden
    • Abstand zwischen zwei parallelen Geraden
    • Abstand zwischen zwei windschiefen Geraden
    • 4 Mini-Tests zu räumlichen Geraden

    • 12 Kursvideos
    • Parameterform
    • Normalform
    • Koordinatenform
    • Punkt auf der Ebene
    • Abstand zwischen Punkt und Ebene
    • Hessesche Normalform
    • Lotfusspunkt
    • Gerade und Ebene
    • Ebene und Ebene: Schnittgerade
    • Schnittwinkel und Abstand
    • 5 Mini-Test zu räumlichen Ebenen

    • 6 Kursvideos
    • Gleichung eines Kreises
    • Gleichung einer Kugel
    • 3 Mini-Tests zu Kreisen und Kugeln

    • Kursvideo
    • Abschluss-Test mit Zertifikat

Kursmaterialien

  • pdf-Script (105 Seiten) zum Ausdrucken oder zur Benutzung auf einem Tablet
  • kurz erklärte Theorie
  • Hervorgehobene, wichtigste Formeln
  • Beispiele, die im Kurs vorgezeigt werden
  • Mini-Übungen zum Selberlösen
  • Auflistung der Lernziele
Script Vorschau

Für wen ist dieser Kurs geeignet?

Der Schwierigkeitsgrad des Kurses ist ideal für Lernende auf der Gymnasialstufe, kurz vor Matura/Abitur. Der Kurs kann auch sehr gut als Vorbereitung für ein Studium oder als Unterstützung für Studierende im ersten Jahr dienen.

David John Brunner

Lehrer für Physik und Mathematik, Zürich

Ich unterrichte mit Leidenschaft und verfolge immer das Ziel, die Inhalte so einfach und so klar wie möglich zu erklären.

Die Kunst liegt darin, die Sache so richtig auf den Punkt zu bringen, so dass sie einleuchtet.

So entsteht Lernerfolg und Motivation!

Was andere sagen

Vielen Dank, sehr angenehm. Ohne Umschweife auf den Punkt gebracht.
Alaudamusic
Absolut perfekt erklärt, ausgezeichnete Beispiele, besten Dank an Sie, Herr Brunner. Werde meine Enkelkinder (Gymnasium) auf Ihren Kanal aufmerksam machen. Muss Ihre Art der Erklärung in höchsten Tönen loben. Danke für Ihr teilen.
gina118
Danke danke danke !!!!! Ich schreibe Morgen die Physik Klausur und hab das mit dem Diagramm nicht ganz verstanden gehabt. Vielen dank! Sehr gut erklärt:)
Jamila M’Barek
Founder, Simply Design
tolles Video :) Ich habe das ganze Thema gleich viel besser verstanden.
Paulina Franiak

TotalTotal Due TodaySubtotalFree TrialAmount Due Zahlung

  • 74 Videos
  • pdf-Script (105 Seiten)
  • 127 Beispiele, Mini-Übungen und Übungsaufgaben (alle mit vollständiger Lösung)
  • 24 Mini-Tests
  • Abschlusstest mit Zertifikat
  • Totaler Zeitbedarf: ca. 30-50 Stunden

CHF 99

Jetzt kaufen

Nicht der richtige Kurs? Geld-Zurück-Garantie!