Euler’scher Polyedersatz
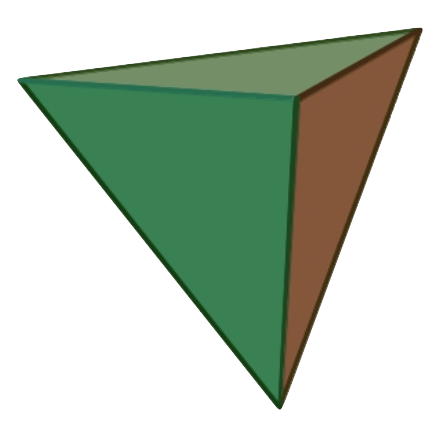
Eulers Polyedersatz geht auf den Schweizer Mathematiker und Physiker Leonhard Euler (1707 – 1783) zurück. Er gilt für jeden konvexen Polyeder, d.h. für jeden dreidimensionalen Körper, der aus vielen Flächen besteht, die durch nach aussen gerichtete Kanten getrennt sind. Der Polyedersatz besagt: \[ E – K + F = 2 \] Dabei sind: Der Euler’sche…