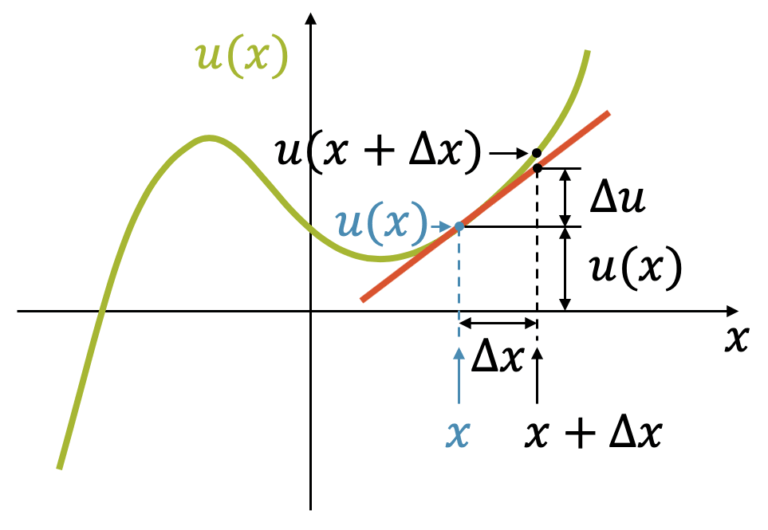Funktionen, die eine Unstetigkeit oder einen Knick aufweisen, sind an der betreffenden Stelle nicht differenzierbar, d.h. die Steigung des Funktionsgraphen (Ableitung der Funktion) kann an dieser Stelle nicht bestimmt werden.
Mit dem Differenzenquotienten wird die Steigung einer Sekante in einem Steigungsdreieck bestimmt. Im Grenzfall des unendlich kleinen Steigungsdreiecks, wird Differenzenquotient zum Differenzialquotient.
Die Ableitungsfunktion gibt die Steigung der Funktion zurück, die abgeleitet worden ist, d.h. der Funktionswert der Ableitungsfunktion ist die Steigung an der betreffenden Stelle.
Durch Ableiten (Differenzieren) einer Funktion, erhalten wir die Ableitungsfunktion. Leiten wir diese Ableitungsfunktion wieder ab, erhalten wir die sog. zweite Ableitung. Durch mehrfaches Ableiten erhalten wir die höheren Ableitungen.
Die Summenregel der Differenzialrechnung besagt, dass die Ableitung einer Summe von Funktionen gleich der Summe der einzelnen abgeleiteten Funktionen ist.
Ein konstanter Faktor kann aus der Funktion herausgenommen und am Schluss dann wieder mit der Ableitungsfunktion multipliziert werden.
Mit der Produktregel kann ein Produkt von zwei Teilfunktionen einzeln abgeleitet und erst am Schluss wieder zu einem Ganzen zusammengeführt werden,
Wir können eigentlich jede Funktion um einen Punkt herum linearisieren, d.h. ihre Tangente in diesem Punkt als Näherungslösung benutzen. In vielen Fällen vereinfacht sich die Rechnung sehr stark. Die Genauigkeit ist oft recht gut, obwohl mit einer viel einfacher zu handhabenden Ersatzfunktion gearbeitet wird.
Analog zur Produktregel, kann auch ein Quotient von zwei Teilfunktionen abgeleitet werden, indem die einzelnen Teilfunktionen abgeleitet werden.
Die Kettenregel kommt dann zum Zug, wenn zwei Funktionen ineinander verschachtelt sind. Mit ihrer Hilfe können solche Verschachtelungen abgeleitet werden, selbst dann, wenn die Verschachtelung mehrfach ist.
Die Integralrechnung befasst sich am Anfang v.a. mit der Berechnung der Fläche unterhalb eines Funktionsgraphen. Die Möglichkeiten, die sich mit der Integralrechnung eröffnen sind aber viel, viel weitgehender als nur Flächenberechnungen. Sie sind sehr vielseitig einsetzbar und von grosser Bedeutung, v.a. in den Natur- und Ingenieurwissenschaften. Wir fangen aber mit der Frage an, wie wir…
Herleitung Wir nehmen das Integral von einer unbekannten unteren Grenze bis zur oberen Grenze . Daraus definieren wir eine Funktion , die dem Argument den Wert des Integrals zuordnet. Damit es kein Problem mit der fixen Grösse gibt, verwenden wir für das Integral die Laufvariable : Jetzt leiten wir diese Funktion nach ab:…
Mit dem unbestimmten Integral ermitteln wir die Stammfunktion. Mit dem bestimmten Integral berechnen wir die Fläche zwischen den Funktionswerten und der -Achse. Wie Flächen aus bestimmten Integralen berechnet werden, schauen wir uns an einem Beispiel an. Gesucht ist die Fläche aus dem folgenden Integral: Die Funktion integrieren wir zuerst in einem unbestimmten Integral,…
Schon bei der Besprechung der Differentialrechnung haben wir eine Faktorregel der Differentialrechnung angetroffen. Das ist natürlich kein Zufall, denn wenn die Integration die Umkehrung der Differentiation ist, dann ist die Summen- und Faktorregel hier mit derjenigen der Differentialrechnung verwandt. Die Faktorregel ist sehr leicht zu erkennen, am besten am Beispiel einer einfachen Summe: …
Analog zur Summenregel der Differenzialrechnung, gibt es auch die Summenregel der Integralrechnung: Ein Integral einer Summe kann auch Summe von zwei Integralen geschrieben werden, mit den beiden Summanden drin.
Vertauschungsregel Wenn wir von rechts nach links, statt von links nach rechts integrieren, arbeiten wir mit statt mit . Deshalb ändert sich das Vorzeichen des Integrals: Wir schauen uns das an einem Beispiel an: Jetzt vertauschen wir die beiden Integrationsgrenzen und rechnen nochmals alles durch: Das Vorzeichen hat tatsächlich…
Du kennst vielleicht die unbestimmten Integrale. Wenn wir sie lösen, erhalten wir die Stammfunktion plus eine Konstante. Im Gegensatz zu den bestimmten Integralen haben unbestimmte Integrale keine Grenzen angegeben. Uneigentliche Integrale haben zwar Grenzen, jedoch ist mindestens eine davon oder . Integrale können beide Grenzen uneigentlich sein und dabei von bis laufen. Folgende Integrale sind…
Für gerade Funktionen kann die Spiegelsymmetrie bezüglich der -Achse ausgenützt werden, wenn die Integrationsgrenzen ebenfalls spiegelsymmetrisch angeordnet sind: Die linke und die rechte Seite sind gleich, d.h. das Integral muss nur auf einer Seite berechnet werden: Ungerade Funktionen sind punktsymmetrisch bezüglich dem Ursprung. Wenn die Integrationsgrenzen ebenfalls symmetrisch angeordnet…
Die Integration durch Substitution ähnelt in ihrer Art der Ableitung mit der Kettenregel. Wir schauen uns das an einem Beispiel an: Beispiel Berechne das folgende Integral: Wir sehen, dass wir hier eine Verschachtelung haben. Die äussere Funktion ist die Wurzel, die innere Funktion ist der lineare Ausdruck . Wir substituieren die innere Funktion…
Partielle Integration für unbestimmte Integrale Die partielle Integration ist eine praktische Integrationsmethode, die angewendet wird, wenn im Integral ein Produkt von zwei Teilfunktionen stehen. Sie muss manchmal mehrfach hintereinander angewendet werden. Die Methode der partiellen Integration wird angewendet, wenn im Integral ein Produkt von zwei Teilfunktionen und steht: In der Formel der…
Gebrochenrationale Funktionen, d.h. Brüche mit einem Polynom im Zähler und einem Polynom im Nenner, sind nicht so einfach zu integrieren. Erstaunlicherweise macht uns v.a. der Zähler Probleme. Integral der einfachen Hyperbelfunktion Die einfache Hyperbelfunktion ist . Wir wissen, dass sie die Ableitung des natürlichen Logarithmus ist: Der natürliche Logarithmus (wie alle…
Bei zeitlich variierenden Grössen, z.B. die Temperatur, ist es von Vorteil sie über eine bestimmte Zeit zu mitteln, z.B. die durchschnittliche Jahrestemperatur. Auf diese Art werden die Schwankungen über die betrachtete Zeitperiode ausgeglichen. Beispiel Die Funktion schwingt zwischen 0 und . Was ist der Mittelwert dieser Funktion über die gesamte Zeit? Der Mittelwert beschreibt die…
In vielen Anwendungen ist es besser, das Quadrat des Funktionswerts zu nehmen, als einfach nur den Funktionswert. Nach der Summenbildung korrigieren wir das Quadrieren wieder, indem wir die Wurzel ziehen. Diese Methode wird vor allem in folgenden Fällen angewendet: Wir schauen uns wieder die Zahlenfolge an, interessieren uns dieses Mal aber für die Quadrate und…
Rotation um die x-Achse Wenn wir den Verlauf einer Funktion um die -Achse rotieren lassen, entsteht ein Rotationskörper gemäss folgender Abbildung. Mit Hilfe der Integralrechnung lässt sich das Volumen dieses Körpers relativ einfach berechnen. Wir betrachten dazu eine unendlich dünne Scheibe (mit der Dicke ). Es handelt sich dabei um einen Zylinder mit Radius und…
Wir erinnern uns nochmals an die Definition des Schwerpunkts: Er vereint die gesamte Masse und ist so platziert, dass er von überall gesehen das gleiche Drehmoment erzeugt, wie die im Körper verteilte Masse. Eine kleine Teilmasse erzeugt eine kleine Teil-Gewichtskraft . Für den ganzen Körper müssen die Teil-Gewichtskräfte integriert werden und wir erhalten die Gewichtskraft:…
Die Integralrechnung wird in der Physik sehr viel gebraucht. Eine typische Anwendung ist für die Berechnung der physikalischen Arbeit von sich verändernden Kräften. Wir beginnen mit einem sehr einfachen Beispiel, das noch ohne Integral auskommen würde, werden daran aber erkennen, wie nützlich die Integralrechnung für etwas kompliziertere Fälle wird. Wir schauen uns zuerst das Beispiel…
Diese Website verwendet Cookies, damit wir dir die bestmögliche Benutzererfahrung bieten können. Cookie-Informationen werden in deinem Browser gespeichert und führen Funktionen aus, wie das Wiedererkennen von dir, wenn du auf unsere Website zurückkehrst, und hilft unserem Team zu verstehen, welche Abschnitte der Website für dich am interessantesten und nützlichsten sind.
Unbedingt notwendige Cookies sollten jederzeit aktiviert sein, damit wir deine Einstellungen für die Cookie-Einstellungen speichern können.
Wenn du diesen Cookie deaktivierst, können wir die Einstellungen nicht speichern. Dies bedeutet, dass du jedes Mal, wenn du diese Website besuchst, die Cookies erneut aktivieren oder deaktivieren musst.
Diese Website verwendet die folgenden zusätzlichen Cookies:
Bitte aktiviere zuerst die unbedingt notwendigen Cookies, damit wir deine Einstellungen speichern können!
