Klicke auf den Titel, um zum gewählten Thema zu gelangen
1-36 von 36 Suchergebnissen
-
Ähnlichkeit
Warum sieht ein Modellauto seinem Original so täuschend ähnlich? In der Geometrie bedeutet Ähnlichkeit, dass Proportionen gewahrt bleiben. Entdecke, wie man durch zentrische Streckung Entfernungen misst, die man eigentlich gar nicht zu Fuss erreichen kann.
Ähnlichkeit
-
Algebraische Funktionen
Wie hängen z.B. Preis und Nachfrage zusammen? Algebraische Funktionen beschreiben diese Beziehungen mathematisch. Ob einfache Geraden oder komplexe Kurven: Sie sind das Werkzeug, um Abhängigkeiten in Natur und Technik präzise darzustellen und vorherzusagen.
Algebraische Funktionen
-
Algebraische Gleichungen
Ein Rätsel um eine unbekannte Zahl? Algebraische Gleichungen sind wie Waagen im Gleichgewicht. Durch geschicktes Umformen isolierst du die unbekannte Variable und löst knifflige Probleme aus Naturwissenschaften und Technik.
Algebraische Gleichungen
-
Bedingte Wahrscheinlichkeit
Verändert eine neue Information die Chance auf einen Gewinn? Die bedingte Wahrscheinlichkeit hilft uns, Risiken neu zu bewerten. Ein Klassiker ist das Monty-Hall-Problem: Manchmal ist es klüger, seine erste Entscheidung noch einmal zu überdenken.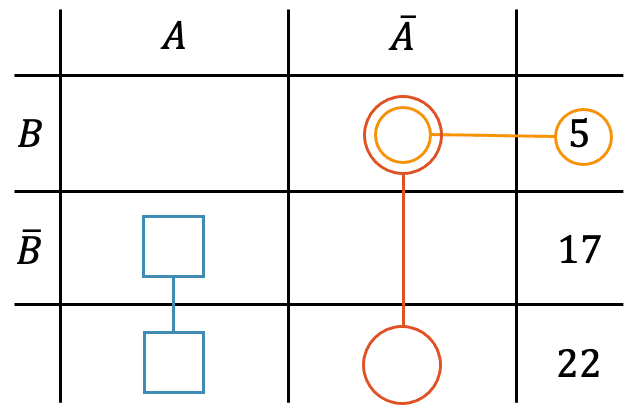
Bedingte Wahrscheinlichkeit
-
Brüche
Brüche dienen der Darstellung von Teilen eines Ganzen und beschreiben präzise Verhältnisse. Durch das Zusammenspiel von Zähler und Nenner ermöglichen sie Berechnungen in Bereichen, in denen natürliche Zahlen für eine exakte Mengenbeschreibung nicht ausreichen.
Brüche
-
Dreiecke
Wusstest du, dass das Dreieck die stabilste Form in der Architektur ist? Von der Statik riesiger Brücken bis hin zur Trigonometrie in der Navigation: Diese einfache Figur mit drei Ecken ist das Fundament unserer modernen Welt.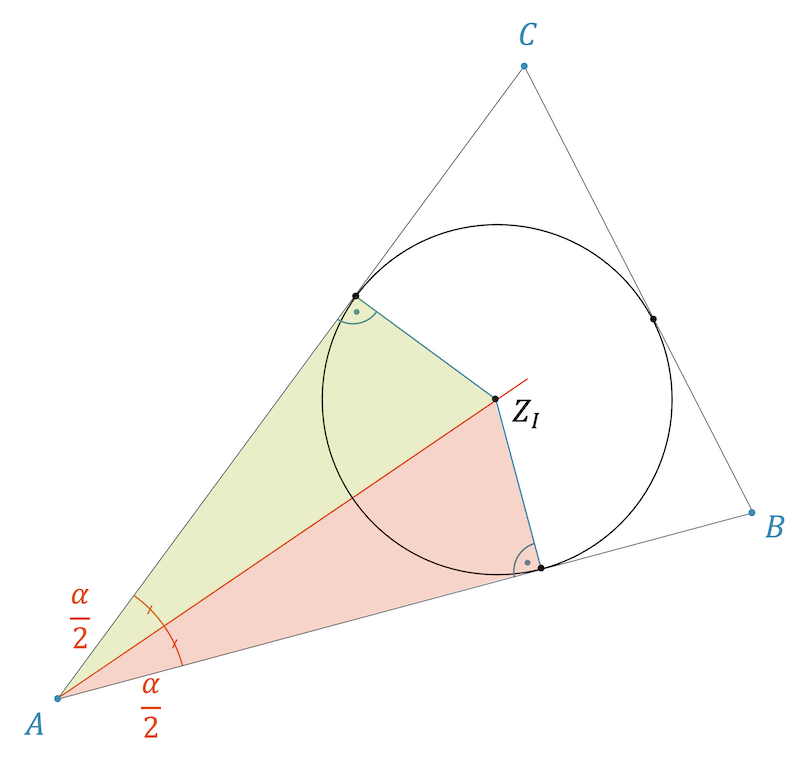
Dreiecke
-
Ereignismengen und Ergebnisraum
Bevor das Glücksrad dreht, sind alle Möglichkeiten offen. Der Ergebnisraum fasst alle denkbaren Ausgänge zusammen. Die Definition von Ereignismengen ist der erste Schritt, um den Zufall berechenbar und die Logik sichtbar zu machen.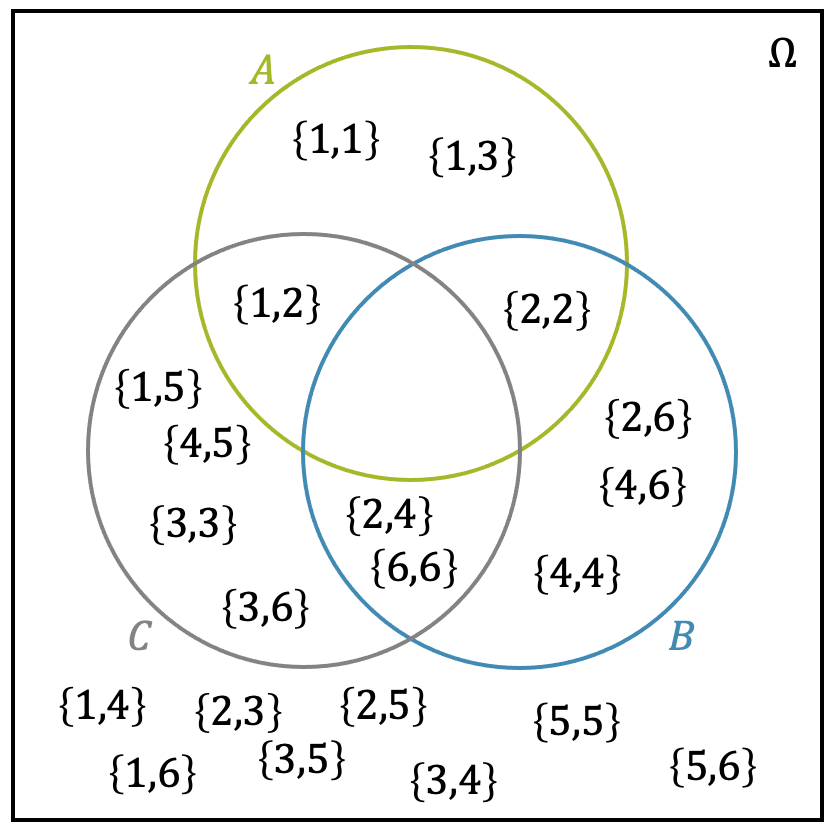
Ereignismengen und Ergebnisraum
-
Exponentialfunktionen
Warum verbreiten sich Nachrichten im Netz so rasant? Exponentialfunktionen beschreiben Prozesse, die immer schneller wachsen. Dieses Modell ist der Schlüssel zum Verständnis von Zinseszins, Bakterienwachstum oder der Dynamik sozialer Medien.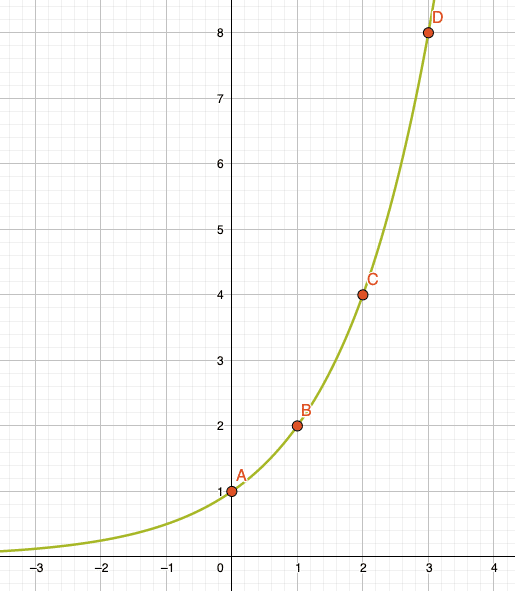
Exponentialfunktionen
-
Folgen
Welche Zahl kommt als Nächstes? Folgen sind geordnete Listen, die oft verblüffenden Mustern folgen. Von der berühmten Fibonacci-Folge in der Natur bis hin zu Grenzwerten führen sie uns tief in die Strukturen der Mathematik.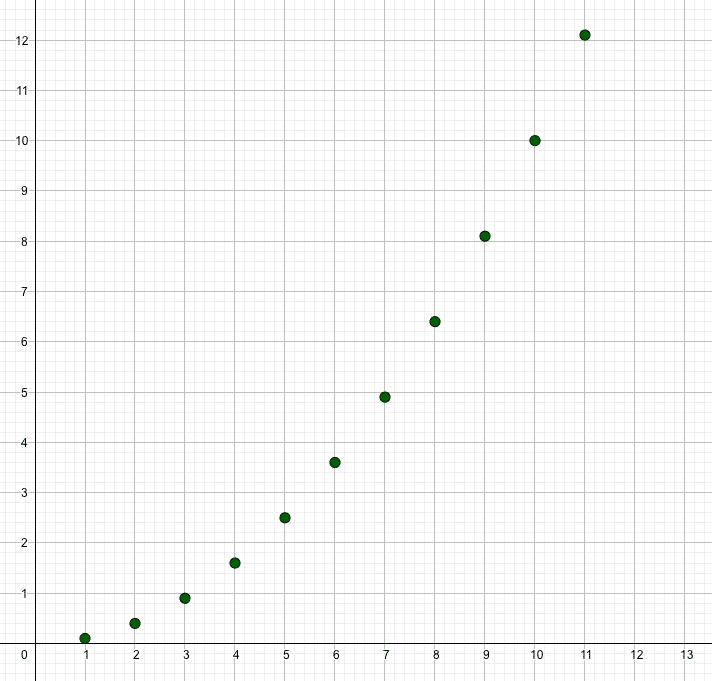
Folgen
-
Funktionen
Funktionen ordnen jedem Eingangswert genau einen Ausgangswert zu. Mit diesem mathematischen Prinzip lassen sich Abhängigkeiten wie die Flugbahn eines Balls oder die Entwicklung von Kosten präzise modellieren und grafisch darstellen.
Funktionen
-
Geometrische Körper
Geometrische Körper sind dreidimensionale Objekte, die durch ihre Begrenzungsflächen definiert sind. Mit Formeln für Volumen und Oberfläche berechnest du z.B. präzise Kapazitäten und Materialstärken, was für Architektur und Fertigungstechnik essenziell ist.
Geometrische Körper
-
Geraden und Ebenen
Im dreidimensionalen Raum beschreiben Geraden und Ebenen die Position von Objekten. Mithilfe von Vektoren lassen sich Schnittpunkte berechnen, was für die Flugbahnberechnung in der Luftfahrt oder die Grafikprogrammierung essenziell ist.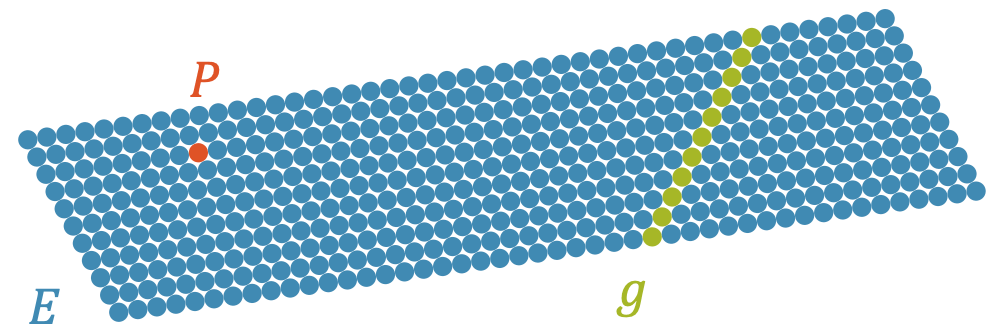
Geraden und Ebenen
-
Gleichungen und Verfahren
Gleichungen sind mathematische Aussagen über die Gleichheit zweier Terme. Durch systematische Lösungsverfahren wie das Äquivalenzumformen findest du unbekannte Grössen in komplexen technischen oder wirtschaftlichen Fragestellungen.
Gleichungen und Verfahren
-
Kombinatorik
Die Kombinatorik untersucht die Anzahl möglicher Anordnungen von Objekten. Ob bei der Sicherheit von Passwörtern oder der Gewinnchance im Lotto: Sie liefert die Basis, um Wahrscheinlichkeiten in diskreten Systemen zu verstehen.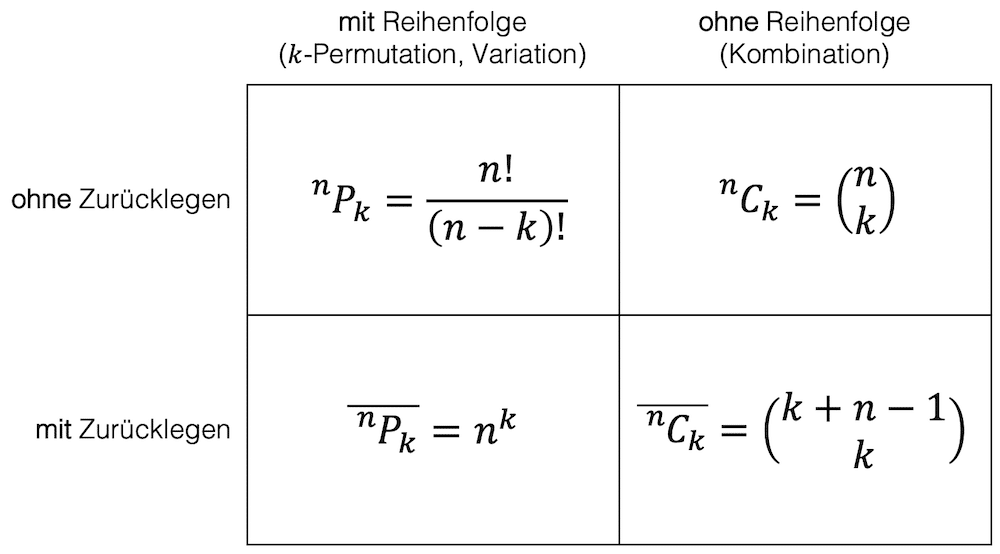
Kombinatorik
-
Kreise
Kreise sind die Mengen aller Punkte mit gleichem Abstand zum jeweiligen Zentrum. Die Zahl π verknüpft den Umfang und Radius und wird zur Grundlage für die Analyse periodischer Schwingungen und runder Bauteile.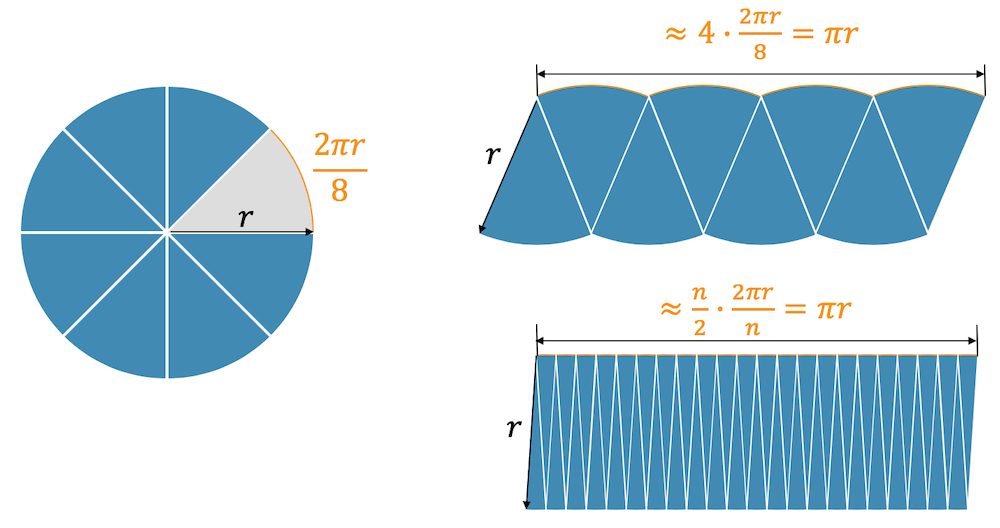
Kreise
-
Lineare Gleichungssysteme (LGS)
Wenn mehrere Bedingungen gleichzeitig erfüllt sein müssen, helfen lineare Gleichungssysteme. Mit Verfahren wie dem Gaus-Algorithmus lassen sich Schnittpunkte von Linien oder Mischverhältnisse in der Chemie exakt bestimmen.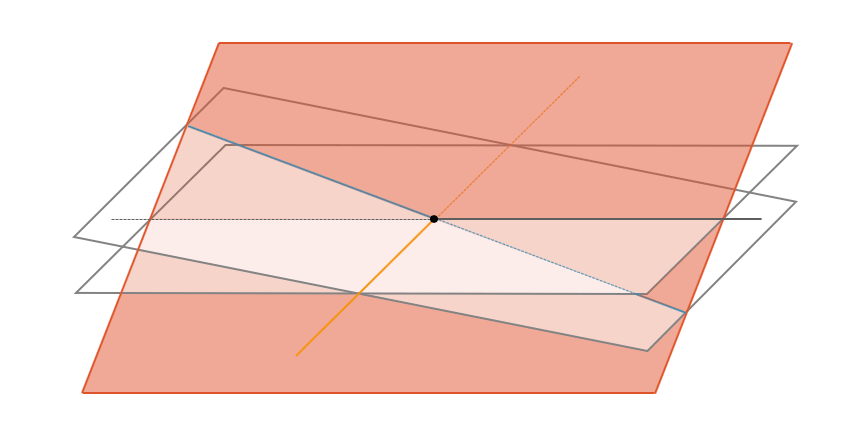
Lineare Gleichungssysteme (LGS)
-
Logarithmus
Der Logarithmus ist die Umkehrfunktion der Exponentialfunktion. Er hilft dir dabei, Zeiträume bei Wachstumsprozessen zu berechnen oder grosse Wertebereiche auf der Dezibel-Skala oder der Richterskala handhabbar zu machen.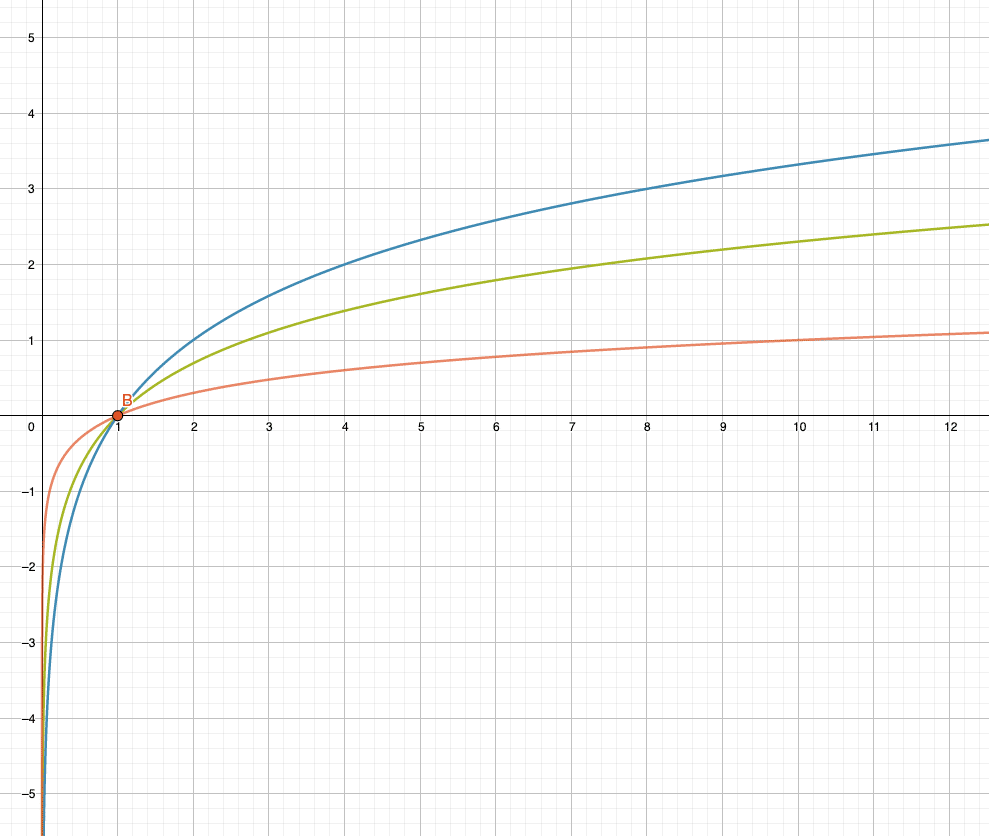
Logarithmus
-
Metrik und Winkel
Metrik und Winkel definieren Abstände und Ausrichtungen im Raum. Sie sind wichtige Werkzeuge, mit denen du z.B. Entfernungen durch blosse Peilung messen kannst, ohne die Strecke physisch zurücklegen zu müssen.
Metrik und Winkel
-
Polyeder
Polyeder sind Körper, die ausschliesslich von ebenen Flächen begrenzt werden. Die Eulersche Polyederformel beschreibt dabei den faszinierenden Zusammenhang zwischen Anzahl Ecken, Kanten und Flächen, der für alle konvexen Polyeder gültig ist.
Polyeder
-
Potenzen
Potenzen dienen der verkürzten Schreibweise einer mehrfachen Multiplikation desselben Faktors. Sie sind die Basis für das Verständnis von Zinseszins-Effekten oder der wissenschaftlichen Darstellung extrem grosser Distanzen im Universum.
Potenzen
-
Produkte von Vektoren
Das Skalarprodukt und das Vektorprodukt (Kreuzprodukt) sind fundamentale Operationen der Vektorrechnung. Sie ermöglichen es dir, Winkel zwischen Kräften exakt zu bestimmen oder Flächeninhalte von Parallelogrammen im dreidimensionalen Raum zu berechnen.
Produkte von Vektoren
-
Prozentrechnen
Prozentrechnen macht Grössenverhältnisse durch den Bezug auf den Grundwert einheitlich vergleichbar. Ob bei Rabatten, Zinsen oder statistischen Erhebungen – es ist das zentrale Werkzeug für die quantitative Beurteilung von Daten.
Prozentrechnen
-
Punkte und Graphen
Im Koordinatensystem lassen sich Wertepaare als Punkte visualisieren. Verbindest du diese zu Funktionsgraphen, werden Trends und Gesetzmässigkeiten sichtbar, die in einer reinen Wertetabelle oft verborgen bleiben.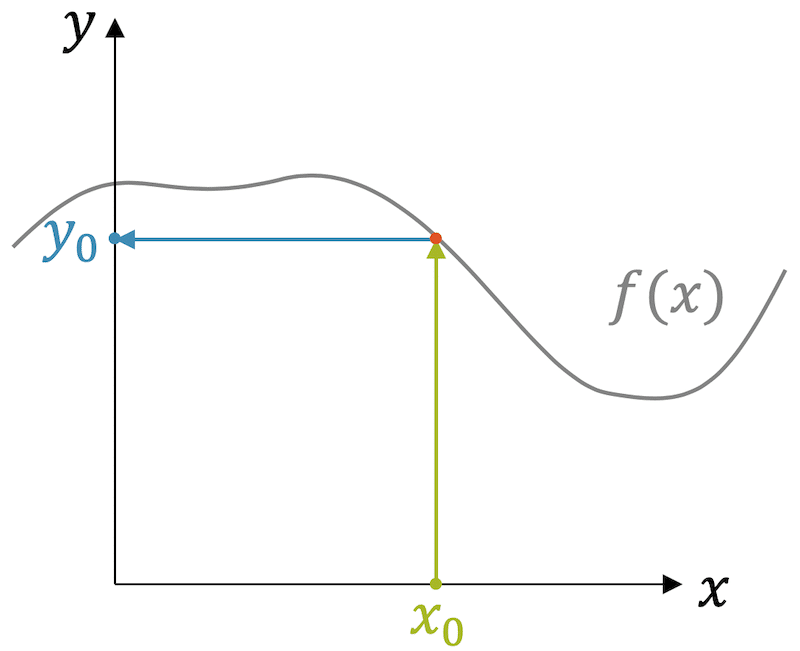
Punkte und Graphen
-
Reihen
Reihen entstehen durch das Aufsummieren der Glieder einer Folge. Besonders spannend sind unendliche Reihen, die trotz unendlich vieler Summanden einen festen, endlichen Grenzwert besitzen können, wie etwa bei geometrischen Reihen.
Reihen
-
Schnitte und Inzidenzen
In der Geometrie beschreiben Schnitte und Inzidenzen die Lagebeziehungen von Objekten. Du erfährst, ob Linien sich kreuzen oder in Punktmengen enthalten sind, was für die computergestützte Konstruktion und Architektur entscheidend ist.
Schnitte und Inzidenzen
-
Statistik
Statistik macht aus Datenmengen nutzbare Informationen. Durch Kennzahlen wie Mittelwert oder Streuung lassen sich Trends in der Wirtschaft objektiv bewerten und Prognosen für zukünftige Entwicklungen auf eine solide Basis stellen.
Statistik
-
Summenzeichen
Das Summenzeichen \(\Sigma\) ermöglicht die kompakte Darstellung langer Additionen. Es ist ein unverzichtbares Symbol der Analysis, um Grenzprozesse oder statistische Gesamtheiten effizient und übersichtlich in mathematischen Formeln festzuhalten.
Summenzeichen
-
Teilung von Strecken
Wie findet man den perfekten Punkt auf einer Linie? Die Teilung von Strecken, etwa im Goldenen Schnitt, ist ein Schlüssel zur Ästhetik und hilft dir, Proportionalitäten in Kunst, Natur und Technik exakt zu bestimmen.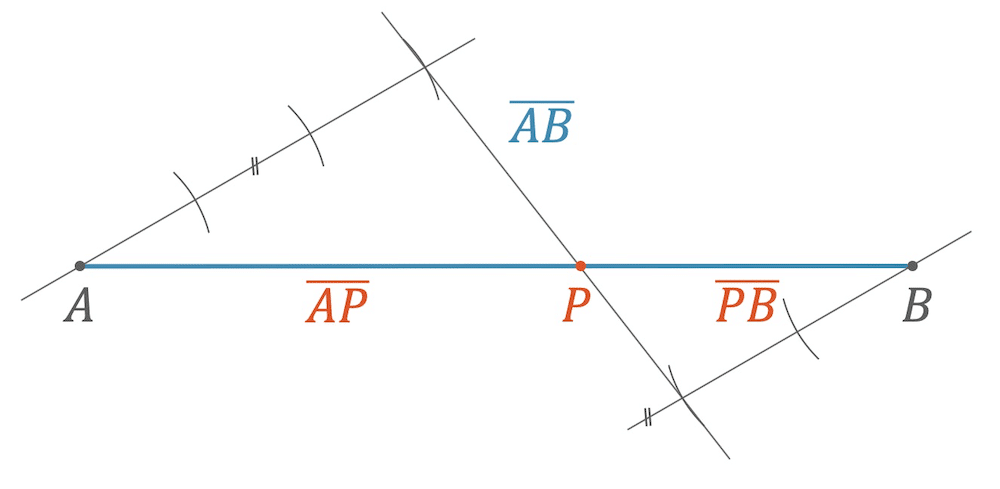
Teilung von Strecken
-
Transzendente Funktionen
Transzendente Funktionen lassen sich nicht durch einfache Algebra ausdrücken. Dazu gehören die Logarithmusfunktion oder Winkelfunktionen, die fundamentale Prozesse wie Zerfall oder Schwingungen in der Physik mathematisch fassbar machen.
Transzendente Funktionen
-
Transzendente Gleichungen
Wenn die Unbekannte im Exponenten oder einer Sinusfunktion steht, suchst du Lösungen für transzendente Gleichungen. Diese erfordern oft Näherungsverfahren, um präzise Ergebnisse für komplexe Probleme der Ingenieurswissenschaften zu liefern.
Transzendente Gleichungen
-
Trigonometrische Funktionen
Sinus, Kosinus und Tangens beschreiben das Verhältnis von Seiten und Winkeln. Mit diesen periodischen Funktionen lassen sich nicht nur Distanzen messen, sondern auch Wellenphänomene in der Akustik und Elektrotechnik berechnen.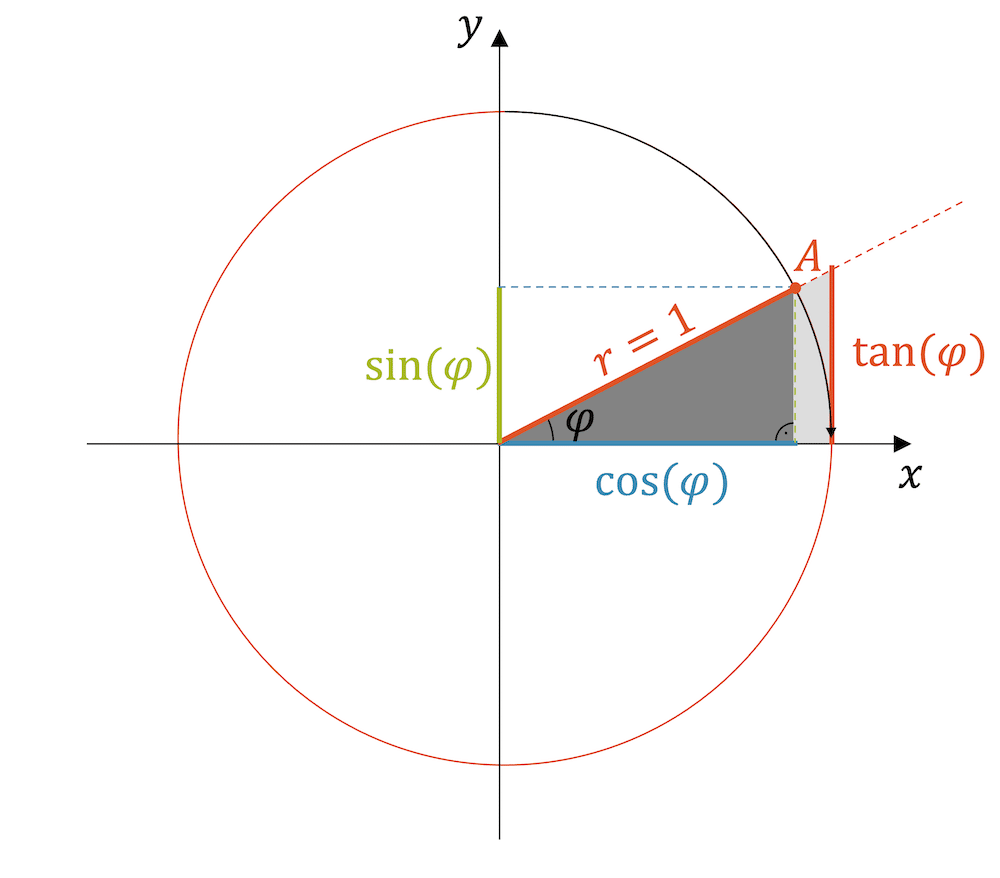
Trigonometrische Funktionen
-
Vektoralgebra
Die Vektoralgebra behandelt gerichtete Grössen im Raum. Sie erlaubt es dir, Verschiebungen und Kräfte rechnerisch zu erfassen, was die Grundlage für jede 3D-Animation und die moderne Navigation per Satellit darstellt.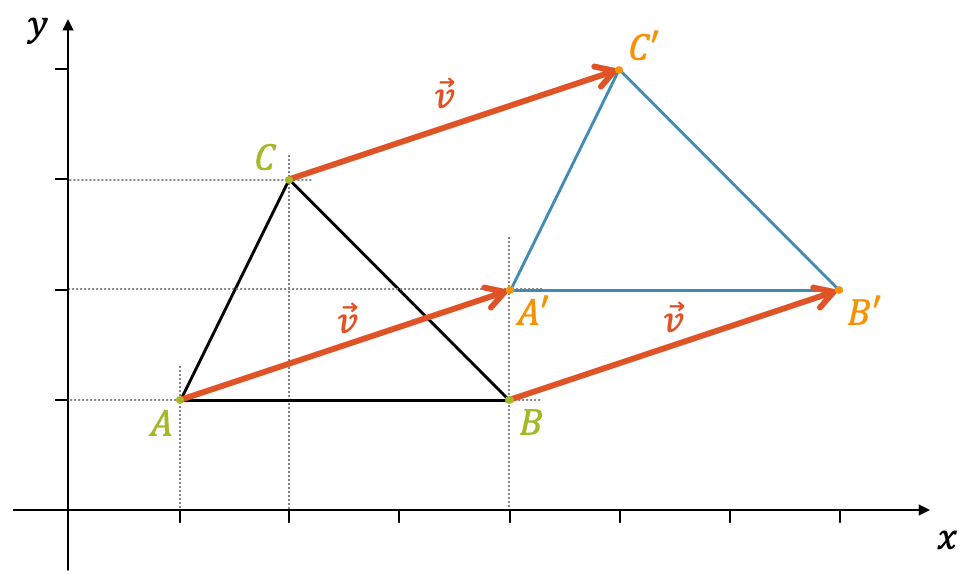
Vektoralgebra
-
Vektoroperationen
Durch Vektoroperationen wie die Addition oder das Skalarprodukt berechnest du resultierende Kräfte. Diese Werkzeuge der linearen Algebra sind essenziell, um Bewegungsabläufe in der Mechanik oder Robotik präzise zu steuern.
Vektoroperationen
-
Wahrscheinlichkeit
Wahrscheinlichkeit quantifiziert die Sicherheit des Eintretens von Ereignissen. Mit dem Gesetz der grossen Zahlen lassen sich Zufälle in der Versicherungsmathematik oder bei Qualitätskontrollen in der Industrie berechenbar machen.
Wahrscheinlichkeit
-
Wurzeln
Wurzeln sind die Umkehrung des Potenzierens und lösen Fragen nach der Basis. Die Quadratwurzel ist beispielsweise notwendig, um aus dem Flächeninhalt eines Quadrats dessen Seitenlänge oder die Diagonale exakt zu bestimmen.
Wurzeln
-
Zufallsgrössen und Verteilungen
Zufallsgrössen ordnen Zufallsergebnissen Zahlenwerte zu. Die Normalverteilung zeigt dabei, wie sich Messwerte natürlicherweise um einen Mittelwert gruppieren, was für die Auswertung von Experimenten und Umfragen zentral ist.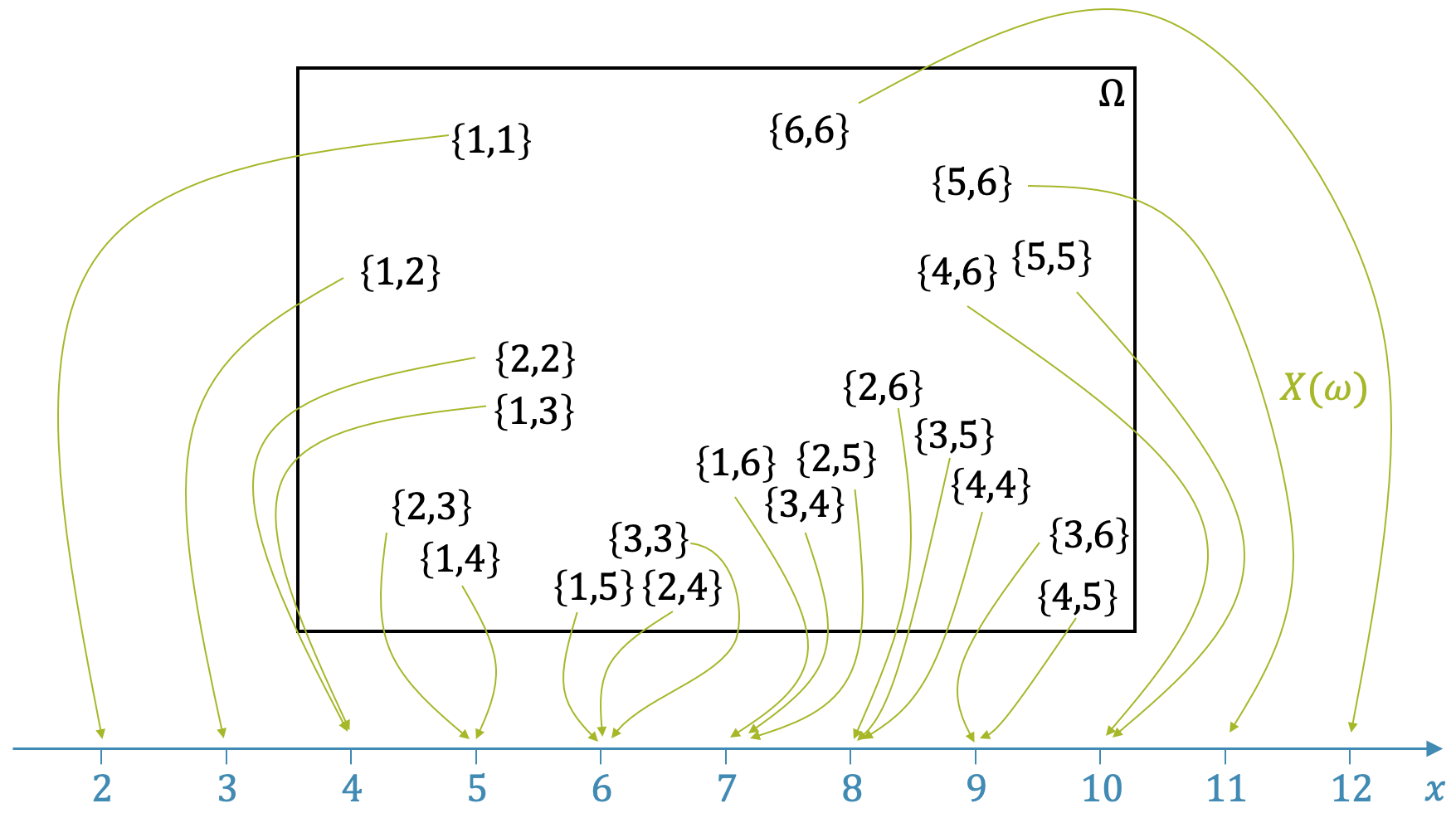
Zufallsgrössen und Verteilungen
