Inhalt
Das Wichtigste in Kürze
Das Volumen einer Pyramide entspricht dem Drittel des Produkts von Grundfläche \(G\) und Höhe \(h\):
\[ V = \frac{1}{3} \cdot G \cdot h \]
Videos
Die Pyramide ist definiert als ein Polygon, das die Grundfläche bildet. Dieses kann regelmässig oder unregelmässig sein. Dann führen die Kanten von den Polygonecken zur Spitze der Pyramide. Oder anders herum: von der Spitze der Pyramide führen Strahlen zu den Ecken des Polygons und bilden die Kanten. Die Pyramide kann gerade oder schief sein.
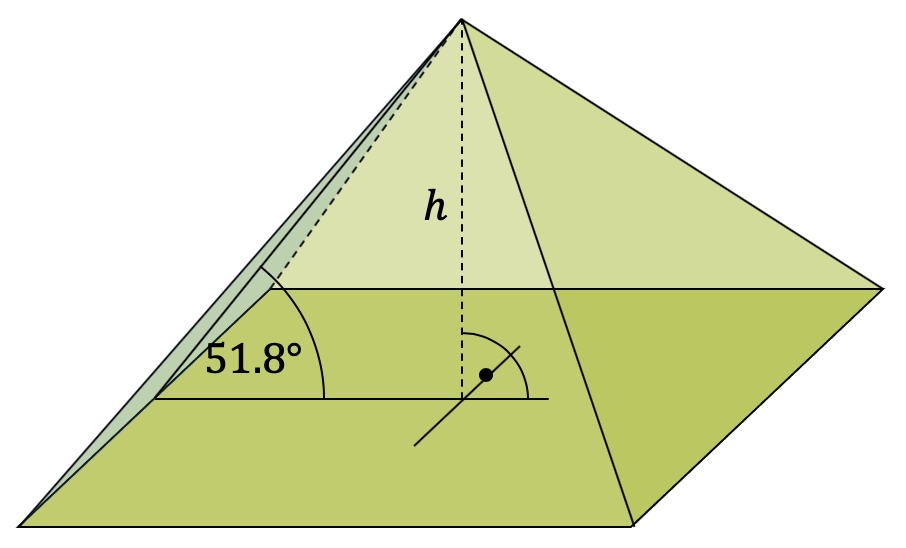
Die uns bekannteste Pyramide ist die ägyptische Pyramide. Die Cheops-Pyramide, die älteste und grösste der drei Pyramiden von Gizeh, hat eine quadratische Grundfläche. Ihre Seitenflächen haben gegenüber der Horizontalen einen Winkel von 51.8°.
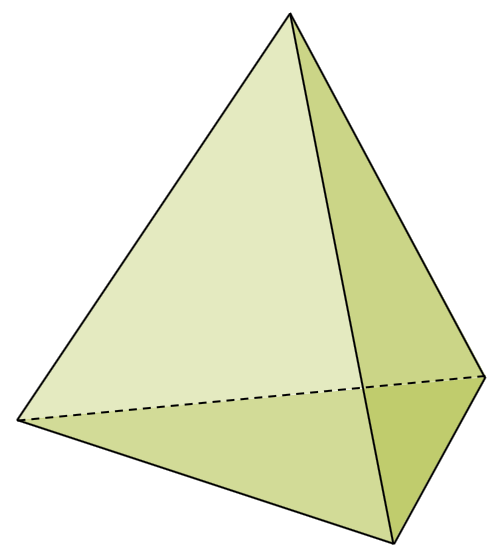
Die Seitenflächen der Pyramide sind alles Dreiecke. Wenn wir vier gleichseitige Dreiecke nehmen und eines davon als Grundfläche benutzen, erhalten wir das ebenfalls bekannte Tetraeder, das zu den platonischen Körpern gehört.
Für die Berechnung des Volumens schauen wir uns einen Würfel an. Wir können ihn drei mal schneiden, so dass drei Pyramiden entstehen. Die drei Schnittebenen sind farbig markiert: rot, grün und blau. Wenn wir nach dem Schnitt die Pyramiden aus dem Würfel herausklappen, sehen wir, dass es drei Pyramiden sind mit der Grundfläche einer Würfelseite. Die Höhe der Pyramiden ist jeweils gleich lang wie eine Würfelkante.
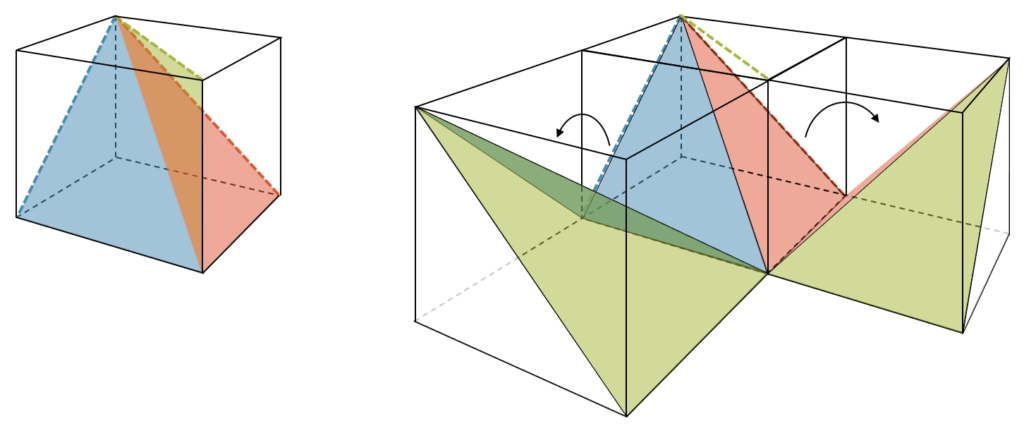
Da wir aus dem Volumen eines Würfels mit Seitenkante \(s\) restlos drei Pyramiden machen konnten und sie alle gleich gross sind, kennen wir ihr Volumen:
\[ V_{\text{Würfel}} = s^3 \quad \rightarrow \quad V_{\text{Pyramide}} = \frac{1}{3} V_{\text{Würfel}} = \frac{1}{3} s^3 \]
Beim Prisma hatten wir gelernt, dass das Volumen der Grundfläche mal der Höhe entspricht. Das hier auch so, d.h. für das Volumen der Pyramiden können wir mit \(G=s^2\) und \(h=s\) folgern:
\[ V_{\text{Würfel}} = \frac{1}{3} s^3 \quad \rightarrow \quad V = \frac{1}{3} \cdot G \cdot h \]
Wir vermuten also, dass bei Pyramiden wir gleich rechnen können, wie bei Prismen, mit dem einzigen Unterschied, dass wir das Produkt von Grundfläche \(G\) und Höhe \(h\) noch dritteln müssen. Das ist jetzt kein allgemein gültiger Beweis, aber in unserem Würfelbeispiel stimmt es. Es ist nun aber so, dass es für alle Pyramiden stimmt, auch für andere Grundflächen und Höhen. Mit dem Prinzip von Cavalieri können wir es wieder auch auf schiefe Körper anwenden.
Das Volumen einer Pyramide entspricht dem Drittel des Produkts von Grundfläche \(G\) und Höhe \(h\):
\[ V = \frac{1}{3} \cdot G \cdot h \]
Beispiel
Gegeben sind die beiden Netze für fünfseitige Pyramiden. Das Netz links spannt eine Pyramide auf. Das Netz rechts aber nicht. Warum?
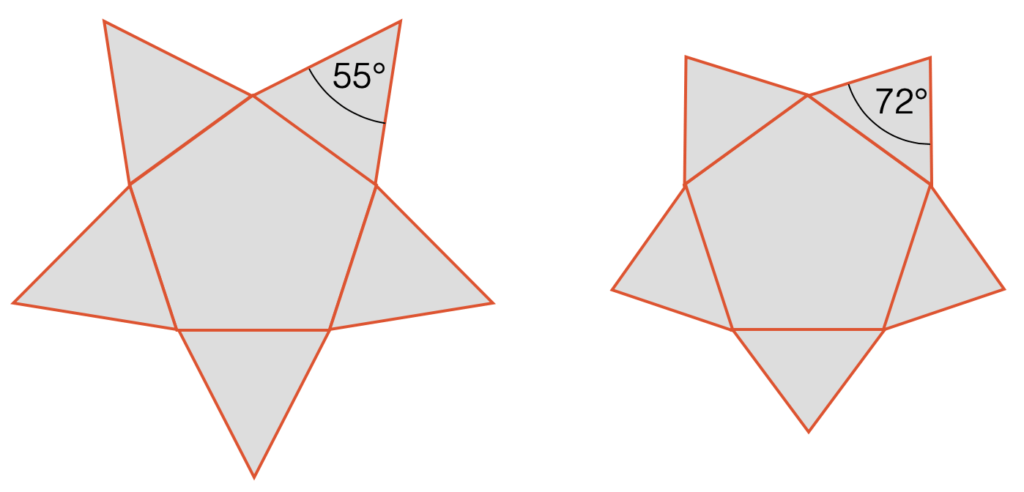
Aufgabensammlung
Mini-Test
Um Zugang zum Mini-Test zu kriegen,
musst du vollwertiges Mitglied im Hacker-Club sein.
publiziert:
überarbeitet:
publiziert:
überarbeitet:
Schreib deine Frage / Kommentar hier unten rein. Ich werde sie beantworten.
Inhalt








Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.